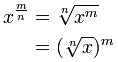Chiamati anche “Radicali” o “Esponenti razionali”
Esponenti interi
Per prima cosa, guardiamo al numero intero esponenti:

L’esponente di un numero dice quante volte usare il numero in una moltiplicazione.
In questo esempio: 82 = 8 × 8 = 64
Un altro esempio: 53 = 5 × 5 × 5 = 125
Esponenti frazionari
Ma cosa succede se l’esponente è una frazione?
|
Un esponente di 12 è effettivamente radice quadrata Un esponente di 13 è radice cubica Un esponente di 14 è la quarta radice E così via! |
 |
Perché?
Vediamo perché in un esempio.
Innanzitutto, le leggi degli esponenti ci dicono come gestire gli esponenti quando moltiplichiamo:
Esempio: x2x2 = (xx) (xx) = xxxx = x4
Che mostra che x2x2 = x (2 + 2) = x4
Quindi proviamo con esponenti frazionari:
Prova un’altra frazione
Riproviamo, ma con un esponente di un quarto (1/4):
Esempio:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Quindi 16¼ usato 4 volte in una moltiplicazione dà 16,
e quindi 16¼ è un 4a radice di 16
Regola generale
Ha funzionato per ½, ha funzionato con ¼, infatti funziona generalmente:
x1 / n = La radice n-esima di x
Quindi possiamo trovare questo:
| |
|
Esempio: cos’è 271/3?
Risposta: 271/3 = ![]() 27 = 3
27 = 3
E le frazioni più complicate?
Che ne dici di un esponente frazionario come 43/2?
Questo in realtà sta dicendo di fare un cubo (3) e una radice quadrata (1/2), in qualsiasi ordine.
Mi spiego.
Una frazione (come m / n) può essere suddivisa in due parti:
- una parte numero intero (m) e
- una frazione (1 / n) part
Quindi, poiché m / n = m × (1 / n) possiamo farlo:
L’ordine non ha importanza, quindi funziona anche per m / n = (1 / n) × m:
E otteniamo questo:
| |
|
Alcuni esempi:
Esempio : Che cos’è 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
o
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
In entrambi i casi si ottiene lo stesso risultato.
Esempio: che cos’è 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
o
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
È stato sicuramente più facile nel secondo modo!
Ora … Gioca con il grafico!
Guarda come cambia dolcemente la curva quando giochi con le frazioni in questa animazione, questo ti mostra che questa idea di esponenti frazionari combacia perfettamente:
Cose da provare:
- Inizia con m = 1 en = 1, poi aumenta lentamente n in modo da poter vedere 1/2, 1/3 e 1/4
- Quindi prova m = 2 e fai scorrere n su e giù per vedere frazioni come 2/3 ecc.
- Ora prova a fare l’esponente -1
- Infine prova ad aumentare m, quindi a ridurre n, quindi a ridurre m, quindi ad aumentare n: la curva dovrebbe girare e girare