La Congettura di Poincaré e altre 6 complesse teorie matematiche sono state soprannominate Millennium Prize Problems dal Clay Mathematics Institute (CMI). Ogni problema è stato descritto come una “importante domanda classica che ha resistito alle soluzioni nel corso degli anni”, con la prima persona che ha ideato una soluzione per ogni guadagno di $ 1.000.000 per gentile concessione del CMI. Tuttavia, come hai visto sopra, risolvere questi problemi non è facile feat. Uno dei problemi è rimasto irrisolto sin dalla sua formulazione nel 1859 dal matematico tedesco Bernhard Riemann.
L’ipotesi di Riemann, dal nome del suddetto matematico tedesco, è ampiamente considerata il problema irrisolto più importante in puro matematica. È di grande interesse per la teoria dei numeri perché implica risultati sulla distribuzione dei numeri primi, che sono usati in tutto, dalla biologia alla crittografia e alla meccanica quantistica. Per comprendere l’ipotesi di Riemann, dobbiamo prima spiegare alcune chiavi concetti:
- Un numero complesso ha la forma a + bi, dove i è definito da i² = -1. In questa forma, la parte reale di un numero complesso è a, e l’immaginario parte è bi.
- La funzione zeta di Riemann è una funzione di una variabile complessa (una funzione di numeri complessi) definita dalla seguente equazione, dove s è qualsiasi numero complesso diverso da 1, e i cui valori sono anch’essi complessi:
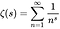
- Uno “zero” di una funzione è una x tale che f (x) = 0
- Gli “zeri banali” della funzione zeta di Riemann sono tutti i numeri interi pari negativi (-2, -4, -6,…)
- Gli “zeri non banali ”Della funzione zeta di Riemann sono tutti gli altri valori di s per cui ζ (s) = 0 (es. s non è un numero intero pari negativo).
Ora che abbiamo alcune definizioni chiare, possiamo andare avanti e affermare l’ipotesi di Riemann:
La parte reale di ogni zero non banale della funzione zeta di Riemann è 1/2
Questo (per me almeno) è molto più facile da capire rispetto alla congettura di Poincaré e non sembra intuitivamente molto difficile. Tuttavia, non sembra nemmeno significare molto. Davvero, chi se ne frega quando questa funzione casuale ha un valore di 0. Non sorprende che molti matematici lo facciano, e per un’ottima ragione.
Alcuni numeri hanno la proprietà speciale di non essere espressi come prodotto di due numeri più piccoli (il prodotto è la moltiplicazione), cioè. 2,3,5,7,11, ecc. Conosciuti come numeri primi, sono in un certo senso i numeri più semplici che puoi ottenere, formando i mattoni per tutti gli altri numeri. Tuttavia, in modo frustrante, i numeri primi non sembrano seguire alcun modello. 3137 è un numero primo, e quello successivo non è fino a 3163, ma poi 3167 e 3169 seguono in rapida successione, che sono tutti numeri primi. In poche parole, se trovi un numero primo, non c’è modo di dire dove sarà il prossimo senza controllare tutti i numeri mentre procedi. Tuttavia, utilizzando il Teorema dei numeri primi (PNT), puoi trovare quanti numeri primi ci sono al di sotto di una certa soglia.
Il Teorema dei numeri primi è solo una stima, con valori diversi che danno una diversa probabilità di essere corretto, ma mai sicuro al 100%. Tuttavia, comprendi l’ipotesi che l’ipotesi di Reimann sia vera, puoi creare un’approssimazione matematica combinando il Teorema dei numeri primi e gli zeri non banali della funzione zeta di Riemann per correggere l’errore delle componenti interne, fornendo il “miglior vincolo possibile” per il termine di errore nel Teorema dei numeri primi. Se fosse possibile dimostrare completamente l’ipotesi di Reimann, questo darebbe al PNT la capacità di fornire stime incredibilmente vicine al valore effettivo, aprendo molte possibilità in diversi rami della matematica. Infatti, ci sono molte ipotesi importanti che stare con “Se l’ipotesi di Riemann è vera, allora …”, quindi risolvere questo problema convaliderebbe immediatamente anche tutte le congetture successive.