학습 목표
- de Broglie 파동 방정식을 설명합니다.
- 사용 움직이는 물체의 파장을 계산하는이 방정식입니다.
보어의 모델을 넘어서
보어의 원자 모델은 전자가 어떻게 에너지를 흡수하고 방출 할 수 있으며 원자 방출 스펙트럼이 어떻게 생성되었는지. 그러나이 모델은 전자가 에너지가 다른 무한 궤도에 존재할 수있는 것이 아니라 고정 된 원형 궤도에만 존재해야하는 이유를 실제로 설명하지 못했습니다. 원자 에너지 상태가 양자화되는 이유를 설명하기 위해 과학자들은 전자의 본질과 그 움직임을 보는 방식을 재고해야했습니다.
뜨거운 물체의 방출 스펙트럼에 대한 플랑크의 조사 그리고 광전 효과에 대한 후속 연구는 빛이 파동과 입자로 작용할 수 있음을 입증했습니다. 전자가 이중 파동 입자 특성을 가질 수 있는지 궁금해하는 것이 합리적이었습니다. 1924 년 프랑스 과학자 Louis de Broglie (1892–1987)는 입자의 파동 특성을 설명하는 방정식을 도출했습니다. 특히 움직이는 물체의 파장 (λ)은 다음과 같이 지정됩니다.
\ displaystyle \ lambda = \ frac {h} {mv}
이 방정식에서 h는 플랑크 상수입니다. , m은 입자의 질량 (kg)이고 v는 입자의 속도 (m / s)입니다. 아래의 문제는 전자의 파장을 계산하는 방법을 보여줍니다.
40m / s의 속도로 던진 0.145kg 야구 공의 파장을 계산한다면 극히 짧은 10-34m 정도의 파장. 이 파장은 첨단 과학 장비로도 감지 할 수 없습니다. 사실, 모든 물체가 파동처럼 움직이는 동안 파장이 너무 짧기 때문에 우리는 그것을 알아 차리지 못합니다. 반면에 측정 가능한 파장을 가진 입자는 모두 매우 작습니다. 그러나 전자의 파동 특성은 전자의 특성에 대한 새로운 이해에서 핵심적인 발전으로 입증되었습니다. 원자핵 주변의 특정 공간에 갇힌 전자는 전자파가 원자의 크기에 정확하게 “맞는”방식으로 만 원자 주위를 이동할 수 있습니다. 즉, 전자파의 주파수가 양자화됩니다. E = hv 방정식에 따라 양자화 된 주파수는 Bohr가 이전에 이론화 한 것처럼 전자가 특정 에너지의 원자에만 존재할 수 있음을 의미합니다.
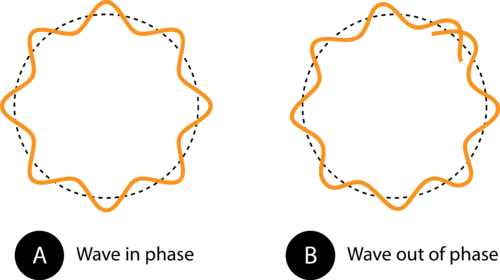
그림 1. (A)의 궤도 둘레는 전자파가 궤도에 완벽하게 맞도록합니다. 이것은 허용 된 궤도입니다. (B)에서 전자파는 그렇지 않습니다. 궤도에 적절하게 적합하므로이 궤도는 허용되지 않습니다.
요약
- deBroglie 파동 방정식을 사용하면 움직이는 모든 파장을 계산할 수 있습니다. 물체.
- 전자의 속도가 감소하면 파장이 증가합니다.
연습
링크 사용 아래를 사용하여 계산을 연습하십시오. deBroglie 파동 방정식 :
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
검토
- 무엇을 Bohr 모델이 설명하지 않았습니까?
- deBroglie 파동 방정식을 설명합니다.
- 전자 속도가 감소하면 어떻게됩니까?