Læringsmål
- Angi de Broglie bølgeligning.
- Bruk denne ligningen for å beregne bølgelengden til et bevegelig objekt.
Utover Bohrs modell
Bohrs modell av atomet var verdifull for å demonstrere hvordan elektroner var i stand til å absorbere og frigjøre energi og hvordan atomemisjonsspekter ble opprettet. Imidlertid forklarte ikke modellen egentlig hvorfor elektroner bare skulle eksistere i faste sirkulære baner i stedet for å kunne eksistere i et ubegrenset antall baner alle med forskjellige energier. For å forklare hvorfor atomenergitilstandene kvantiseres, trengte forskere å tenke på nytt hvordan de så på naturen til elektronet og dets bevegelse.
Plancks undersøkelse av emisjonsspektrene til varme gjenstander og de påfølgende studiene av den fotoelektriske effekten hadde bevist at lys var i stand til å oppføre seg både som en bølge og som en partikkel. Det virket rimelig å lure på om elektroner også kunne ha dobbel bølgepartikkel. I 1924 utledet den franske forskeren Louis de Broglie (1892–1987) en ligning som beskrev bølgenaturen til enhver partikkel. Spesielt er bølgelengden (λ) til ethvert bevegelig objekt gitt av:
\ displaystyle \ lambda = \ frac {h} {mv}
I denne ligningen er h Plancks konstant , m er massen av partikkelen i kg, og v er partikkelens hastighet i m / s. Problemet nedenfor viser hvordan man skal beregne bølgelengden til elektronet.
Hvis vi skulle beregne bølgelengden til en 0.145 kg baseball kastet med en hastighet på 40 m / s, ville vi komme med en ekstremt kort bølgelengde i størrelsesorden 10−34 m. Denne bølgelengden er umulig å oppdage selv med avansert vitenskapelig utstyr. Faktisk, mens alle objekter beveger seg med bølgelignende bevegelse, legger vi aldri merke til det fordi bølgelengdene er altfor korte. På den annen side er partikler med målbare bølgelengder veldig små. Imidlertid viste bølgenaturen til elektronet seg å være en nøkkelutvikling i en ny forståelse av elektronets natur. Et elektron som er begrenset til et bestemt rom rundt atomets kjerne kan bare bevege seg rundt det atomet på en slik måte at elektronbølgen «passer» riktig på atomets størrelse. Dette betyr at frekvensen til elektronbølger blir kvantifisert. Basert på E = hv-ligningen betyr de kvantiserte frekvensene at elektroner bare kan eksistere i et atom ved spesifikke energier, slik Bohr tidligere hadde teoretisert.
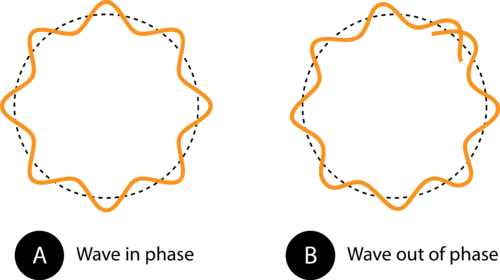
Figur 1. Omkretsen til banen i (A) gjør at elektronbølgen passer perfekt inn i banen. Dette er en tillatt bane. I (B), gjør ikke elektronbølgen passe ordentlig inn i banen, så denne banen er ikke tillatt.
Sammendrag
- DeBroglie-bølgelikningene tillater beregning av bølgelengden til enhver bevegelse objekt.
- Når elektronens hastighet synker, øker bølgelengden.
Øv
Bruk lenken nedenfor for å øve på beregninger ved hjelp av deBroglie bølgeligning:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Review
- Hva forklarte ikke Bohr-modellen?
- Angi deBroglie-bølgeligningen.
- Hva skjer når elektronens hastighet synker?