Het vermoeden van Poincaré en zes andere complexe wiskundige theorieën zijn door het Clay Mathematics Institute (CMI) de Millenniumprijsproblemen genoemd. Elk probleem is beschreven als een “belangrijke klassieke vraag die in de loop der jaren geen oplossingen heeft gevonden”, waarbij de eerste persoon die een oplossing bedacht voor elk $ 1.000.000 verdiende dankzij de CMI. Zoals u hierboven zag, is het oplossen van deze problemen echter niet eenvoudig feat. Een van de problemen is onopgelost gebleven sinds de formulering in 1859 door de Duitse wiskundige Bernhard Riemann.
De Riemann-hypothese, genoemd naar de eerder genoemde Duitse wiskundige, wordt algemeen beschouwd als het belangrijkste onopgeloste probleem in pure vorm. wiskunde. Het is van groot belang in de getaltheorie omdat het resultaten impliceert over de verdeling van priemgetallen, die in alles worden gebruikt, van biologie tot codering en kwantummechanica.Om de Riemann-hypothese te begrijpen, moeten we eerst een paar belangrijke concepten:
- Een complex getal heeft de vorm a + bi, waarbij i wordt gedefinieerd door i² = -1. In deze vorm is het reële deel van een complex getal a, en het imaginaire deel is bi.
- De Riemann-zetafunctie is een functie van een complexe variabele (een functie van complexe getallen) gedefinieerd door de volgende vergelijking, waarbij s een willekeurig complex getal anders dan 1 is, en waarvan de waarden ook complex zijn:
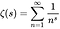
- Een “nul” van een functie is een x zodat f (x) = 0
- De “triviale nullen” van de Riemann-zetafunctie zijn alle negatieve even gehele getallen (-2, -4, -6,…)
- De “niet-triviale nullen ”Van de Riemann-zetafunctie zijn alle andere waarden van s waarvoor ζ (s) = 0 (dwz. s is geen negatief zelfs geheel getal).
Nu we een aantal definities hebben gepat, kunnen we doorgaan en de Riemann-hypothese vermelden:
Het reële deel van elke niet-triviale nul van de Riemann-zetafunctie is 1/2
Deze (voor mij tenminste) is een stuk gemakkelijker te begrijpen dan het vermoeden van Poincaré en lijkt intuïtief niet erg moeilijk. Het lijkt echter ook niet veel te betekenen. Echt, wat maakt het uit wanneer deze willekeurige functie de waarde 0 heeft. Het is niet verrassend dat veel wiskundigen dat wel doen, en om een heel goede reden.
Sommige getallen hebben de speciale eigenschap dat ze niet kunnen worden uitgedrukt als het product van twee kleinere getallen (product is vermenigvuldiging), dwz. 2,3,5,7,11, enz. Bekend als priemgetallen, ze zijn in zekere zin de eenvoudigste getallen die je kunt krijgen en vormen de bouwstenen voor alle andere getallen. Frustrerend genoeg lijken priemgetallen geen enkel patroon te volgen. 3137 is een priemgetal, en het volgende daarna is pas 3163, maar dan volgen 3167 en 3169 elkaar snel op, die allemaal priemgetallen zijn. Kort samengevat, als u één priemgetal vindt, is er geen manier om te zeggen waar het volgende zal zijn zonder alle cijfers te controleren. Met behulp van de priemgetalstelling (PNT) kun je echter achterhalen hoeveel priemgetallen er onder een bepaalde drempel zijn.
De priemgetalstelling is slechts een schatting, met verschillende waarden die een andere kans geven om correct, maar nooit 100% zekerheid. Begrijp echter de veronderstelling dat de Reimann-hypothese waar is, u kunt een wiskundige benadering maken door de priemgetalstelling en de niet-triviale nullen van de Riemann-zetafunctie te combineren om fouten in de interne componenten te corrigeren, waardoor de ‘best mogelijke’ grens voor de foutterm in de priemgetalstelling. Als het mogelijk zou zijn om de Reimann-hypothese volledig te bewijzen, zou dit de PNT de mogelijkheid geven om ongelooflijk dichte schattingen te geven van de werkelijke waarde, wat veel mogelijkheden zou openen in verschillende takken van de wiskunde. er zijn veel belangrijke hypothesen dat het zijn met “Als de Riemann-hypothese waar is, dan…”, dus het oplossen van dit probleem zou onmiddellijk alle volgende vermoedens valideren.