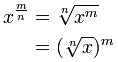Ook wel “radicalen” of “rationele exponenten” genoemd.
Geheel getal exponenten
Laten we eerst eens kijken naar het hele getal exponenten:

De exponent van een getal geeft aan hoe vaak het getal moet worden gebruikt in een vermenigvuldiging.
In dit voorbeeld: 82 = 8 × 8 = 64
Een ander voorbeeld: 53 = 5 × 5 × 5 = 125
Fractionele exponenten
Maar wat als de exponent een breuk is?
|
Een exponent van 12 is eigenlijk vierkantswortel Een exponent van 13 is kubuswortel Een exponent van 14 is de 4e wortel Enzovoort! |
 |
Waarom?
Laten we eens kijken waarom in een voorbeeld.
Ten eerste vertellen de wetten van exponenten ons hoe we omgaan met exponenten wanneer we vermenigvuldigen:
Voorbeeld: x2x2 = (xx) (xx) = xxxx = x4
Wat aantoont dat x2x2 = x (2 + 2) = x4
Laten we dat dus proberen met fractionele exponenten:
Probeer een andere breuk
Laten we dat nog eens proberen, maar met een exponent van een kwart (1/4):
Voorbeeld:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Dus 16¼ 4 keer gebruikt in een vermenigvuldiging geeft 16,
en dus 16¼ is een 4e wortel van 16
Algemene regel
Het werkte voor ½, het werkte met ¼, in feite werkt het over het algemeen:
x1 / n = De n-de wortel van x
Dus we kunnen dit bedenken:
| |
|
Voorbeeld: wat is 271/3?
Antwoord: 271/3 = ![]() 27 = 3
27 = 3
Hoe zit het met meer gecompliceerde breuken?
Hoe zit het met een fractionele exponent zoals 43/2?
Dat is eigenlijk zeggen om een kubus (3) en een vierkantswortel (1/2) in willekeurige volgorde te doen.
Laat me het uitleggen.
Een breuk (zoals m / n) kan in twee delen worden opgesplitst:
- een geheel getaldeel (m), en
- een breuk (1 / n) deel
Dus, omdat m / n = m × (1 / n) kunnen we dit doen:
De volgorde doet er niet toe, dus het werkt ook voor m / n = (1 / n) × m:
En we krijgen dit:
| |
|
Enkele voorbeelden:
Voorbeeld : Wat is 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
of
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
In beide gevallen krijgt u hetzelfde resultaat.
Voorbeeld: wat is 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
of
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Het was zeker gemakkelijker op de 2e manier!
Nu … Speel met de grafiek!
Zie hoe vloeiend de curve verandert als je speelt met de breuken in deze animatie laat zien dat dit idee van fractionele exponenten goed bij elkaar past:
Dingen om te proberen:
- Begin met m = 1 en n = 1, en verhoog dan langzaam n zodat je 1/2, 1/3 en 1/4 kunt zien
- Probeer dan m = 2 en schuif n op en neer om breuken zoals 2/3 enz. te zien
- Probeer nu de exponent -1 te maken.
- Probeer ten slotte m te verhogen, vervolgens n te verkleinen, vervolgens m te verkleinen en vervolgens n te verhogen: de curve moet rond en rond gaan