Wat is standaarddeviatie?STDEV.P | STDEV.S | Variantie
Op deze pagina wordt uitgelegd hoe u de standaarddeviatie berekent op basis van de gehele populatie met behulp van de STDEV.P-functie in Excel en hoe u de standaarddeviatie schat op basis van een steekproef met de STDEV.S-functie in Excel.
Wat is standaarddeviatie?
Standaarddeviatie is een getal dat aangeeft hoe ver getallen verwijderd zijn van hun gemiddelde.
1. De onderstaande getallen hebben bijvoorbeeld een gemiddelde (gemiddelde) van 10.
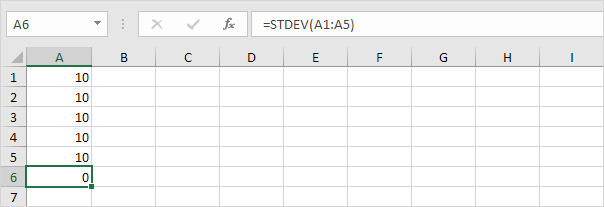
Uitleg: de getallen zijn allemaal hetzelfde die betekent dat er geen variatie is. Als resultaat hebben de getallen een standaarddeviatie van nul. De STDEV-functie is een oude functie. Microsoft Excel raadt het gebruik van de nieuwe STEDV.S-functie aan die exact hetzelfde resultaat oplevert.
2. De onderstaande getallen hebben ook een gemiddelde (gemiddelde) van 10.
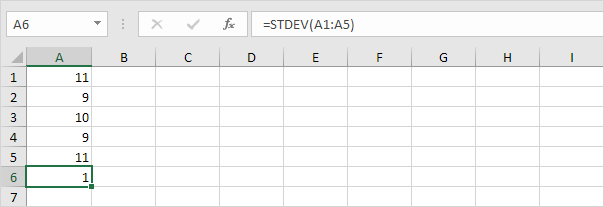
Toelichting: de getallen liggen dicht bij het gemiddelde. Hierdoor hebben de getallen een lage standaarddeviatie.
3. Onderstaande getallen hebben ook een gemiddelde (gemiddelde) van 10.
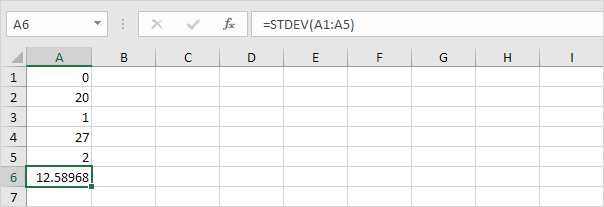
Uitleg: de cijfers zijn uitgespreid. Hierdoor hebben de cijfers een hoge standaarddeviatie.
STDEV.P
De functie STDEV.P (de P staat voor Population) in Excel berekent de standaarddeviatie op basis van de gehele populatie. U geeft bijvoorbeeld les aan een groep van 5 studenten. Je hebt de testscores van alle studenten. De gehele populatie bestaat uit 5 datapunten. De STDEV.P-functie gebruikt de volgende formule:
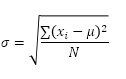
In dit voorbeeld x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (gemiddeld), N = 5 (aantal datapunten).
1. Bereken het gemiddelde (μ).
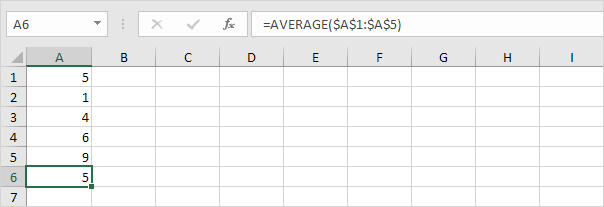
2. Bereken voor elk getal de afstand tot het gemiddelde.
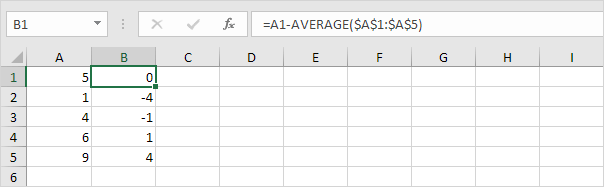
3. Kwadrateer deze afstand voor elk getal.
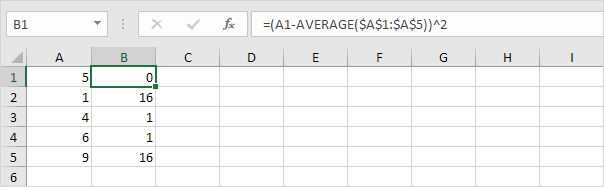
4. Som (∑) deze waarden op.
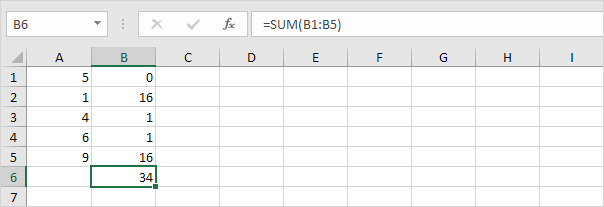
5. Deel door het aantal gegevenspunten (N = 5).
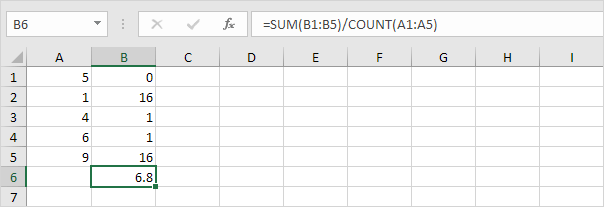
6. Neem de vierkantswortel.
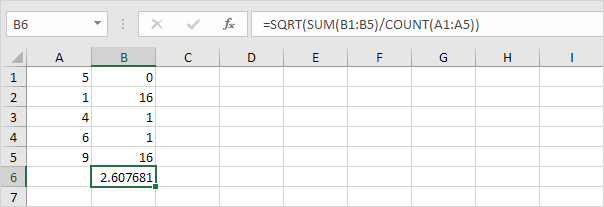
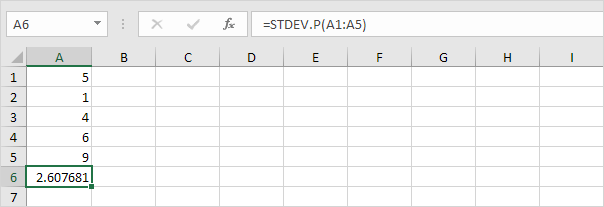
7. Gelukkig kan de STDEV.P-functie in Excel al deze stappen voor u uitvoeren.
STDEV.S
De STDEV.S-functie (de S staat voor Sample) in Excel schat de standaarddeviatie op basis van een steekproef. U geeft bijvoorbeeld les aan een grote groep studenten. U heeft slechts de testscores van 5 studenten. De steekproefomvang is gelijk aan 5. De STDEV.S-functie gebruikt de volgende formule:
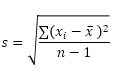
In dit voorbeeld x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (dezelfde nummers als hierboven), x ̄ = 5 (voorbeeld gemiddelde), n = 5 (steekproefomvang).
1. Herhaal stap 1-5 hierboven, maar deel bij stap 5 door n-1 in plaats van N.
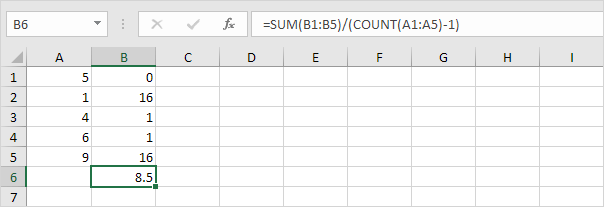
2. Neem de vierkantswortel.
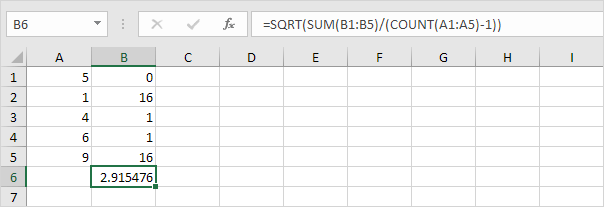
3. Gelukkig kan de STDEV.S-functie in Excel al deze stappen voor u uitvoeren.
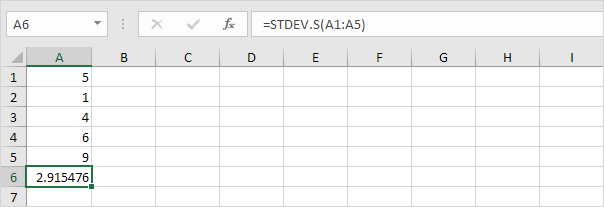
Opmerking: waarom delen we door n – 1 in plaats van door n wanneer we de standaarddeviatie schatten op basis van een steekproef? Bessel’s correctie stelt dat delen door n-1 in plaats van door n een betere schatting van de standaarddeviatie geeft.
Variantie
Variantie is het kwadraat van de standaarddeviatie. Zo simpel is het. Soms is het gemakkelijker om de variantie te gebruiken bij het oplossen van statistische problemen.
1. De onderstaande VAR.P-functie berekent de variantie op basis van de gehele populatie.
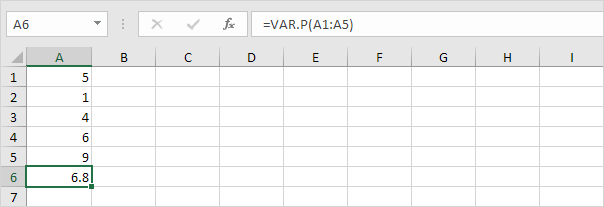
Opmerking: je wist dit antwoord al (zie stap 5 onder STDEV.P). Neem de vierkantswortel van dit resultaat om de standaarddeviatie te vinden op basis van de hele populatie.
2. De onderstaande VAR.S-functie schat de variantie op basis van een steekproef.
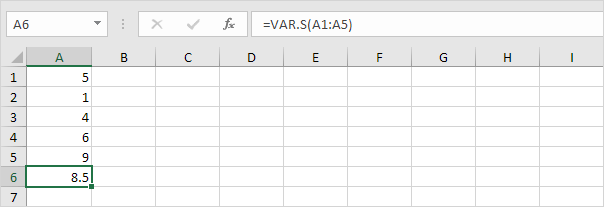
Opmerking: u wist dit antwoord al (zie stap 1 onder STDEV.S). Neem de vierkantswortel van dit resultaat om de standaarddeviatie te vinden op basis van een steekproef.
3. VAR en VAR.S geven exact hetzelfde resultaat.
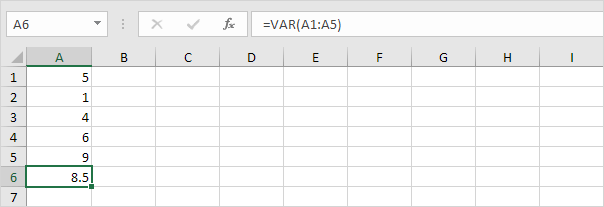
Opmerking: Microsoft Excel raadt het gebruik van de nieuwe VAR.S-functie aan.