Cele nauczania
- Podaj równanie falowe de Brogliego.
- Użyj to równanie do obliczenia długości fali poruszającego się obiektu.
Poza modelem Bohra
Model atomu Bohra był cenny w zademonstrowaniu, jak elektrony były w stanie pochłaniać i uwalniać energię oraz tworzyć widma emisji atomowej. Jednak model tak naprawdę nie wyjaśniał, dlaczego elektrony powinny istnieć tylko na ustalonych kołowych orbitach, zamiast być w stanie istnieć na nieograniczonej liczbie orbit o różnych energiach. Aby wyjaśnić, dlaczego stany energii atomowej są kwantowane, naukowcy musieli przemyśleć sposób, w jaki postrzegali naturę elektronu i jego ruch.
Badanie Plancka widm emisyjnych gorących obiektów a późniejsze badania efektu fotoelektrycznego dowiodły, że światło może zachowywać się zarówno jako fala, jak i jako cząstka. Wydawało się rozsądne, aby zastanowić się, czy elektrony mogą mieć również naturę cząstek o podwójnej fali. W 1924 r. Francuski naukowiec Louis de Broglie (1892–1987) wyprowadził równanie opisujące falową naturę dowolnej cząstki. W szczególności długość fali (λ) dowolnego poruszającego się obiektu jest określona wzorem:
\ Displaystyle \ lambda = \ Frac {h} {mv}
W tym równaniu h jest stałą Plancka , m to masa cząstki w kg, a v to prędkość cząstki wm / s. Poniższy problem pokazuje, jak obliczyć długość fali elektronu.
Gdybyśmy obliczyli długość fali piłki bejsbolowej o wadze 0,145 kg rzucanej z prędkością 40 m / s, otrzymalibyśmy niezwykle krótki długość fali rzędu 10−34 m. Tej długości fali nie można wykryć nawet przy użyciu zaawansowanego sprzętu naukowego. Rzeczywiście, podczas gdy wszystkie obiekty poruszają się ruchem przypominającym fale, nigdy tego nie zauważamy, ponieważ długości fal są o wiele za krótkie. Z drugiej strony wszystkie cząstki o mierzalnych długościach fal są bardzo małe. Jednak falowa natura elektronu okazała się kluczowym krokiem w nowym zrozumieniu natury elektronu. Elektron, który jest ograniczony do określonej przestrzeni wokół jądra atomu, może poruszać się wokół tego atomu tylko w taki sposób, że jego fala elektronowa „pasuje” do rozmiaru atomu, co oznacza, że częstotliwości fal elektronowych są kwantowane. Opierając się na równaniu E = hv, kwantowane częstotliwości oznaczają, że elektrony mogą istnieć w atomie tylko przy określonych energiach, zgodnie z teorią Bohra.
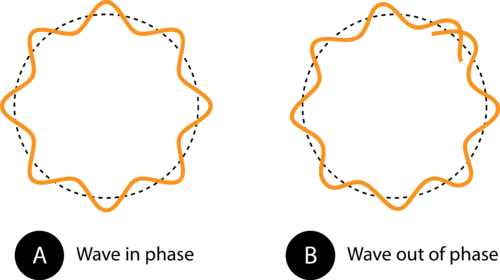
Rysunek 1. Obwód orbity w (A) umożliwia idealne dopasowanie fali elektronowej do orbity. Jest to dozwolona orbita. W (B) fala elektronowa nie pasują prawidłowo do orbity, więc ta orbita jest niedozwolona.
Podsumowanie
- Równania falowe deBroglie pozwalają na obliczenie długości fali dowolnego ruchu obiekt.
- Wraz ze spadkiem prędkości elektronu zwiększa się jego długość fali.
Ćwicz
Użyj łącza poniżej, aby przećwiczyć obliczenia przy użyciu równanie fali deBrogliego:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Recenzja
- Co czy model Bohra nie wyjaśnił?
- Podaj równanie falowe deBrogliego.
- Co się dzieje, gdy prędkość elektronu spada?