Ce este abaterea standard? | STDEV.P | STDEV.S | Varianță
Această pagină explică cum se calculează abaterea standard pe baza întregii populații utilizând funcția STDEV.P în Excel și cum se estimează abaterea standard pe baza unui eșantion utilizând funcția STDEV.S în Excel.
Ce este abaterea standard?
Abaterea standard este un număr care vă arată cât de departe sunt numerele de media lor.
1. De exemplu, numerele de mai jos au o medie (medie) de 10.
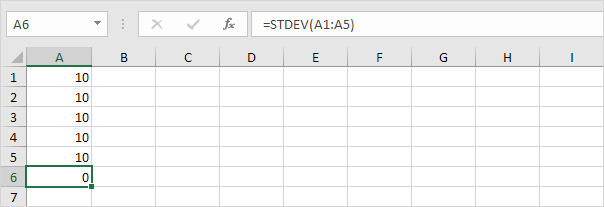
Explicație: numerele sunt la fel înseamnă că nu există nicio variație. Ca rezultat, numerele au o abatere standard de zero. Funcția STDEV este o funcție veche. Microsoft Excel recomandă utilizarea noii funcții STEDV.S care produce exact același rezultat.
2. Numerele de mai jos au, de asemenea, o medie (medie) de 10.
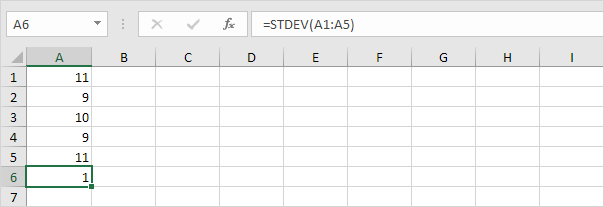
Explicație: numerele sunt apropiate de medie. Ca urmare, numerele au o abatere standard scăzută.
3. Numerele de mai jos au, de asemenea, o medie (medie) de 10.
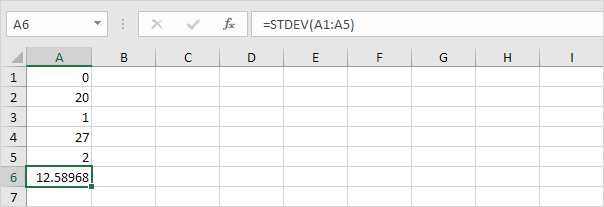
Explicație: numerele sunt răspândite. Ca urmare, numerele au o abatere standard ridicată.
STDEV.P
Funcția STDEV.P (P înseamnă Populație) în Excel calculează abaterea standard pe baza întregii populații. De exemplu, predai un grup de 5 studenți. Aveți scorurile testelor tuturor studenților. Întreaga populație este formată din 5 puncte de date. Funcția STDEV.P folosește următoarea formulă:
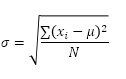
În acest exemplu, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (medie), N = 5 (numărul de puncte de date).
1. Calculați media (μ).
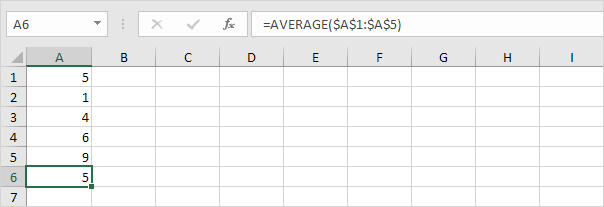
2. Pentru fiecare număr, calculați distanța până la medie.
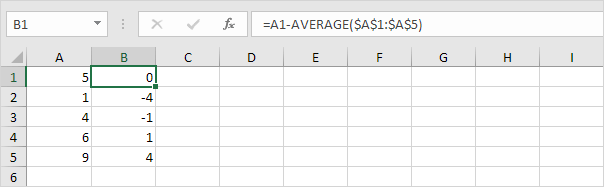
3. Pentru fiecare număr, pătrează această distanță.
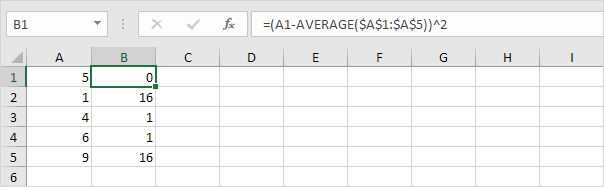
4. Sumați (∑) aceste valori.
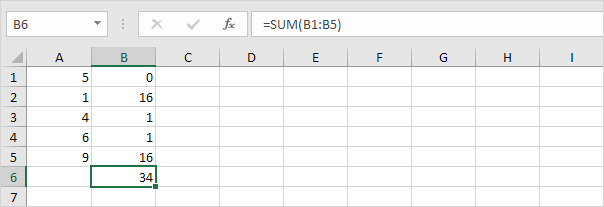
5. Împărțiți la numărul de puncte de date (N = 5).
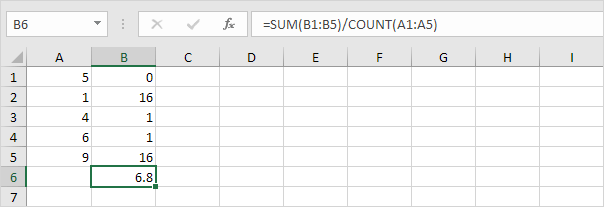
6. Luați rădăcina pătrată.
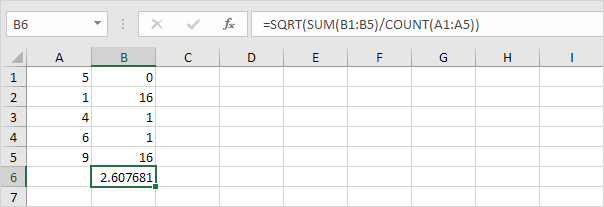
7. Din fericire, funcția STDEV.P din Excel poate executa toți acești pași.
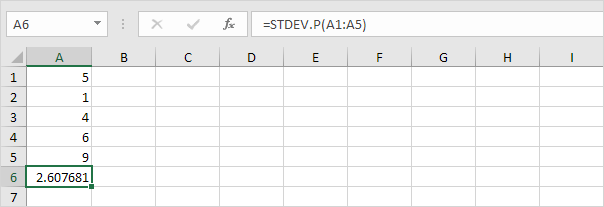
STDEV.S
Funcția STDEV.S (S reprezintă Sample) în Excel estimează abaterea standard pe baza unui sample. De exemplu, predați un grup mare de studenți. Aveți doar scorurile testelor de 5 elevi. Dimensiunea eșantionului este egală cu 5. Funcția STDEV.S folosește următoarea formulă:
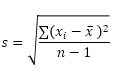
În acest exemplu, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (aceleași numere ca mai sus), x̄ = 5 (eșantion medie), n = 5 (dimensiunea eșantionului).
1. Repetați pașii 1-5 de mai sus, dar la pasul 5 împărțiți cu n-1 în loc de N.
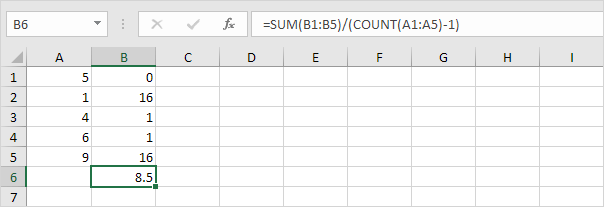
2. Luați rădăcina pătrată.
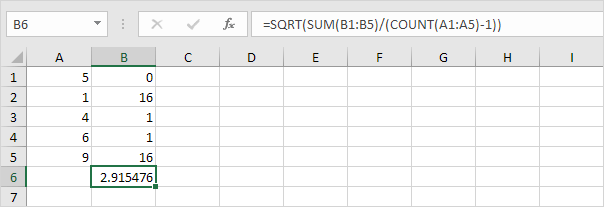
3. Din fericire, funcția STDEV.S din Excel poate executa toți acești pași.
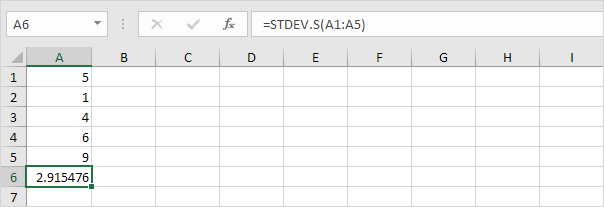
Notă: de ce împărțim la n – 1 în loc de n când estimăm abaterea standard pe baza unui eșantion? Corecția lui Bessel afirmă că împărțirea la n-1 în loc de la n oferă o estimare mai bună a abaterii standard.
Varianța
Varianța este pătratul abaterii standard. Este atât de simplu. Uneori este mai ușor să folosiți varianța atunci când rezolvați probleme statistice.
1. Funcția VAR.P de mai jos calculează varianța pe baza întregii populații.
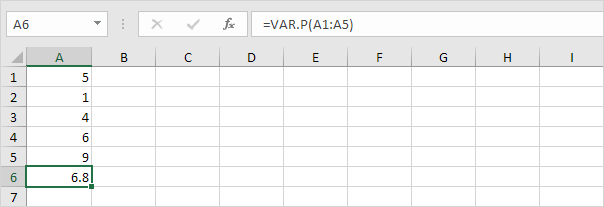
Notă: știați deja acest răspuns (consultați pasul 5 sub STDEV.P). Luați rădăcina pătrată a acestui rezultat pentru a găsi abaterea standard pe baza întregii populații.
2. Funcția VAR.S de mai jos estimează varianța pe baza unui eșantion.
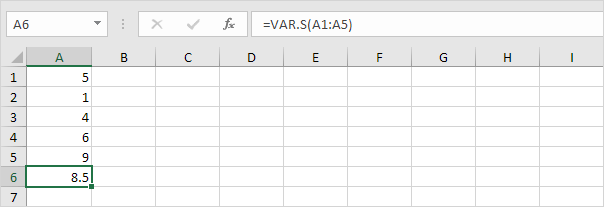
Notă: știați deja acest răspuns (consultați pasul 1 sub STDEV.S). Luați rădăcina pătrată a acestui rezultat pentru a găsi abaterea standard pe baza unui eșantion.
3. VAR și VAR.S produc exact același rezultat.
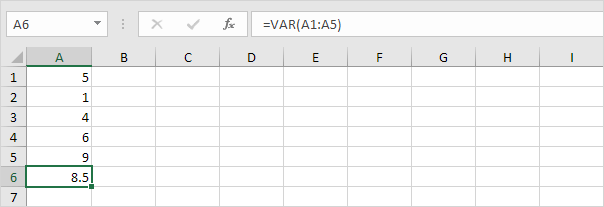
Notă: Microsoft Excel recomandă utilizarea noii funcții VAR.S.