Conjectura Poincaré și alte 6 teorii matematice complexe au fost denumite Millennium Prize Problems de către Clay Mathematics Institute (CMI). Fiecare problemă a fost descrisă ca o „întrebare clasică importantă care a rezistat soluțiilor de-a lungul anilor”, prima persoană care a conceput o soluție pentru fiecare câștigând 1.000.000 USD, datorită CMI. Cu toate acestea, așa cum ați văzut mai sus, rezolvarea acestor probleme nu este ușoară. Una dintre probleme a rămas nerezolvată de când a fost formulată în 1859 de către matematicianul german Bernhard Riemann.
Ipoteza Riemann, numită după matematicianul german menționat mai sus, este considerată a fi cea mai importantă problemă nerezolvată în este de mare interes în teoria numerelor, deoarece implică rezultate despre distribuția numărului prim, care sunt utilizate în orice, de la biologie la criptare și mecanica cuantică. Pentru a înțelege ipoteza Riemann, trebuie mai întâi să explicăm câteva chei concepte:
- Un număr complex este de forma a + bi, unde i este definit de i² = -1. În această formă, partea reală a unui număr complex este a, iar imaginarul partea este bi.
- Funcția zeta Riemann este o funcție a unei variabile complexe (o funcție a numerelor complexe) definită de următoarea ecuație, unde s este orice număr complex altul decât 1 și ale cărui valori sunt, de asemenea, complexe:
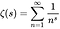
- Un „zero” al unei funcții este un x astfel încât f (x) = 0
- „zerourile banale” ale funcției zeta Riemann sunt toate numerele pare negative (-2, -4, -6, …)
- „zerourile non-banale ”Din funcția zeta Riemann sunt toate celelalte valori ale lui s pentru care ζ (s) = 0 (adică. s nu este un număr întreg negativ).
Acum că avem câteva definiții în jos pat, putem merge mai departe și să afirmăm ipoteza Riemann:
Partea reală a fiecărui zero non-trivial al funcției zeta Riemann este 1/2
Acesta (pentru mine cel puțin) este mult mai ușor de înțeles decât Conjectura Poincaré și nu pare intuitiv foarte dificil. Cu toate acestea, nu pare să însemne prea mult. Într-adevăr, cui îi pasă când această funcție aleatorie are o valoare de 0. Ei bine, nu este surprinzător, o mulțime de matematicieni o fac și dintr-un motiv foarte bun.
Unele numere au proprietatea specială că nu pot fi exprimate ca produs al a două numere mai mici (produsul fiind multiplicare), adică. 2,3,5,7,11 etc. Cunoscute ca numere prime, acestea sunt într-un anumit sens cele mai simple numere pe care le puteți obține, formând elementele de bază pentru toate celelalte numere. În mod frustrant, numerele prime nu par să urmeze niciun model. 3137 este un număr prim, iar următorul după acesta nu este până la 3163, dar apoi 3167 și 3169 urmează în succesiune rapidă, toate fiind prime. Pe scurt, dacă găsiți un număr prim, nu există nicio modalitate de a spune unde urmează să fie următorul fără a verifica toate numerele pe măsură ce mergeți. Cu toate acestea, folosind teorema numărului prim (PNT), puteți găsi câte numere prime există sub un anumit prag.
Teorema numărului prim este doar o estimare, cu valori diferite care oferă o probabilitate diferită de a fi corect, dar niciodată 100% siguranță. Cu toate acestea, înțelegeți ipoteza că ipoteza Reimann este adevărată, puteți crea o aproximare matematică care combină teorema numărului prim și zerourile non-banale ale funcției zeta Riemann pentru a corecta erorile componentelor interne, oferind „cel mai bun posibil” legat de termenul de eroare din teorema numărului primar. Dacă ar fi posibil să se demonstreze complet ipoteza Reimann, acest lucru i-ar oferi PNT capacitatea de a furniza estimări incredibil de apropiate de valoarea reală, deschizând multe posibilități în diferite ramuri ale matematicii. De fapt, există multe ipoteze importante care spun că „dacă ipoteza Riemann este adevărată, atunci…”, deci rezolvarea acestei probleme ar valida instantaneu și toate conjecturile ulterioare.