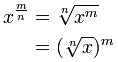Numiți și „Radicali” sau „Exponenți raționali”
Exponenți cu număr întreg
Mai întâi, să analizăm numărul întreg exponenți:

Exponentul unui număr indică de câte ori se folosește numărul într-o multiplicare.
În acest exemplu: 82 = 8 × 8 = 64
Un alt exemplu: 53 = 5 × 5 × 5 = 125
Exponenți fracționari
Dar dacă exponentul este o fracție?
|
Un exponent de 12 este de fapt rădăcină pătrată Un exponent de 13 este rădăcină cub Un exponent de 14 este a 4-a rădăcină Și așa mai departe! |
 |
De ce?
Să vedem de ce într-un exemplu.
Mai întâi, Legile Exponenților ne spun cum să gestionăm exponenții atunci când înmulțim:
Exemplu: x2x2 = (xx) (xx) = xxxx = x4
Ceea ce arată că x2x2 = x (2 + 2) = x4
Deci, să încercăm asta cu exponenți fracționari:
Încercați o altă fracțiune
Să încercăm din nou, dar cu un exponent de un sfert (1/4):
Exemplu:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Deci 16¼ folosit de 4 ori într-o înmulțire dă 16,
și deci 16¼ este un A 4-a rădăcină a lui 16
Regula generală
A funcționat ½, a funcționat cu ¼, de fapt funcționează în general:
x1 / n = A n-a rădăcină a lui x
Deci putem veni cu acest lucru:
| |
|
Exemplu: Ce este 271/3?
Răspuns: 271/3 = ![]() 27 = 3
27 = 3
Dar fracțiile mai complicate?
Dar un exponent fracționat precum 43/2?
Asta înseamnă într-adevăr să faci un cub (3) și o rădăcină pătrată (1/2), în orice ordine.
Lasă-mă să explic.
O fracție (cum ar fi m / n) poate fi împărțită în două părți:
- o parte cu număr întreg (m) și
- o fracție (1 / n) partea
Deci, deoarece m / n = m × (1 / n) putem face acest lucru:
Ordinea nu contează, deci funcționează și pentru m / n = (1 / n) × m:
Și obținem acest lucru:
| |
|
Câteva exemple:
Exemplu : Ce este 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
sau
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
Oricum, obține același rezultat.
Exemplu: Ce este 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
sau
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
A fost cu siguranță mai ușor a doua cale!
Acum … Joacă-te cu graficul!
Vezi cât de lin se schimbă curba când joci cu fracțiile din această animație, aceasta vă arată că această idee de exponenți fracționari se potrivește frumos:
Lucruri de încercat:
- Începeți cu m = 1 și n = 1, apoi creșteți încet n astfel încât să puteți vedea 1/2, 1/3 și 1/4
- Apoi încercați m = 2 și glisați n sus și jos pentru a vedea fracțiuni precum 2/3 etc.
- Acum încercați să faceți exponentul -1
- În cele din urmă, încercați să măriți m, apoi să reduceți n, apoi să reduceți m, apoi să măriți n: curba ar trebui să meargă în jur și în jur