Uitați tot ce știți despre numere.
De fapt, uitați că știți chiar ce este un număr.
Acest lucru de aici începe matematica.
În loc de matematică cu cifre, ne vom gândi acum la matematică cu „lucruri”.
Definiție
Ce este un set? Ei bine, pur și simplu puneți, este „o colecție.
Mai întâi specificăm o proprietate comună printre„ lucruri ”(definim acest cuvânt mai târziu) și apoi adunăm toate„ lucrurile ”care au această proprietate comună.

De exemplu, articolele pe care le porți: pălărie, cămașă, jachetă, pantaloni și așa mai departe.
Sunt sigur că ați putea veni cu cel puțin o sută.
Acest lucru este cunoscut ca un set.
|
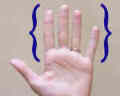
Sau un alt exemplu sunt tipurile de degete. Acest set include index, mijloc, inel și roz. |
 |
Deci, sunt doar lucruri grupate împreună cu o anumită proprietate în comun.
Notare
Există o notație destul de simplă pentru seturi. Pur și simplu enumerăm fiecare element (sau „membru”) separat printr-o virgulă, apoi punem câteva paranteze cretate în jurul întregului lucru:

Parantezele crețate {} sunt uneori numite „paranteze setate” sau „paranteze”.
Aceasta este notația pentru cele două exemple anterioare:
{șosete, pantofi, ceasuri, cămăși, …}
{index, middle, ring, pinky}
Observați cum primul exemplu are „…” (trei puncte împreună) .
Cele trei puncte … sunt numite puncte de suspensie și înseamnă „continuați pe”.
Deci asta înseamnă că primul exemplu continuă .. . pentru infinit.
(OK, nu există într-adevăr o cantitate infinită de lucruri pe care să le poți purta, dar nu sunt deloc sigur de asta! După o oră de gândire la diferite lucruri, eu „m încă nu sunt sigur. Deci, să spunem că este infinit pentru acest exemplu.)
Deci:
Dar uneori „…” poate fi folosit în mijloc pentru a salva scrierea listelor lungi:
Exemplu: setul de litere:
{a, b, c, .. ., x, y, z}
În acest caz este un set finit (există doar 26 de litere, nu?)
Seturi numerice
Deci, ce legătură are asta cu matematica? Când definim un set, tot ce trebuie să specificăm este o caracteristică comună. Cine spune că nu putem face acest lucru cu numerele?
Și așa mai departe. Putem veni cu toate tipurile diferite de seturi.
De asemenea, putem defini un set după proprietățile sale, cum ar fi {x | x > 0} care înseamnă „setul tuturor x-urilor, astfel încât x este mai mare de 0”, consultați Set-Builder Notation pentru a afla mai multe.
Și putem avea seturi de numere care nu au nici o proprietate comună, acestea fiind definite doar în acest fel. De exemplu:
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203 }
Sunt toate seturile pe care tocmai le-am lovit în mod aleatoriu pe tastatura mea pentru a le produce.
De ce sunt seturile importante?
Seturile sunt proprietatea fundamentală a matematicii. Acum, ca un cuvânt de avertizare, seturile, de la sine, par destul de inutile. Dar numai atunci când aplicăm seturi în situații diferite, ele devin elementul puternic al matematicii care sunt.
Matematica se poate complica uimitor destul de repede. Teoria graficelor, Algebra abstractă, Analiza reală, Complexul Analiză, Algebră liniară, Teoria numerelor și lista continuă. Dar există un lucru pe care toate îl împărtășesc în comun: Seturi.
Set Universal
 |
La început am folosit cuvântul „lucruri” între ghilimele. Numim acest lucru setul universal. Este „un set care conține totul. Ei bine, nu tocmai totul. Tot ce este relevant pentru întrebarea noastră. |
|
 |
În teoria numerelor, setul universal este toate numerele întregi, deoarece teoria numerelor este pur și simplu studiu al numerelor întregi. |
|
 |
Dar în Calcul (cunoscut și ca analiză reală), setul universal este aproape întotdeauna numerele reale. |
|
 |
Și, într-o analiză complexă, ați ghicit, setul universal este numărul numerelor complexe. |
Mai multe notări
 |
Când vorbim despre seturi, este destul de standard să folosiți litere majuscule pentru a reprezenta setul și litere mici pentru a reprezenta un element din acel set. Deci, de exemplu, A este un set și a este un eleme nt în A. La fel cu B și b, și C și c. |
Acum nu trebuie să ascultați standardul , puteți utiliza ceva de genul m pentru a reprezenta un set fără a încălca legile matematice (atenție, puteți obține π ani în închisoare la matematică pentru a împărți la 0), dar această notație este destul de drăguță și ușor de urmat, așa că de ce nu?
De asemenea, când spunem că un element a se află într-un set A, folosim simbolul ![]() pentru a-l arăta.
pentru a-l arăta.
Și dacă ceva nu este într-un set use ![]() .
.
Exemplu: Setul A este {1,2,3}. Putem vedea că 1 ![]() A, dar 5
A, dar 5 ![]() A
A
Egalitate
Două seturi sunt egale dacă au exact aceiași membri. Acum, la prima vedere s-ar putea să nu pară egali, deci este posibil să trebuiască să-i examinăm atent!
Exemplu: Sunt A și B egali unde:
- A este setul ai cărui membri sunt primele patru numere întregi pozitive
- B = {4, 2, 1, 3}
Să verificăm. Ambele conțin 1. Amândouă conțin 2. Și 3, Și 4. Și am verificat fiecare element al ambelor seturi, deci: Da, sunt egale!
Și semnul egal ( =) este folosit pentru a arăta egalitatea, așa că scriem:
A = B

Subseturi
Când definim un set, dacă luăm bucăți din acel set, putem forma ceea ce se numește un subset.
În general:
A este un subset de B dacă și numai dacă fiecare element al lui A se află în B.
Deci, să folosim această definiție în unele exemple.
Să încercăm un exemplu mai dificil.
Subseturi adecvate
Dacă ne uităm la definiția subseturilor și ne lăsăm mintea să rătăcească puțin, ajungem la un ciudat concluzie.
Fie A un set. Este fiecare element al lui A în A?
Ei, umm, da, desigur, nu?
Deci asta înseamnă că A este un subset al lui A. Este un subset al lui!
Acest lucru nu pare foarte corect, nu-i așa? Dacă vrem ca subseturile noastre să fie adecvate, introducem (ce altceva decât) subseturi adecvate:
A este un subset corespunzător al lui B dacă și numai dacă fiecare elementul A este, de asemenea, în B și există cel puțin un element în B care nu este în A.
Această mică bucată de la sfârșit este acolo pentru a vă asigura că A nu este un subset corespunzător în sine: spunem că B trebuie să aibă cel puțin un element suplimentar.
Exemplu:
{1, 2, 3} este un subset al lui {1, 2, 3}, dar nu este un subset corespunzător de {1, 2, 3}.
Exemplu:
{1, 2, 3} este un subset corespunzător al lui {1, 2, 3, 4} deoarece elementul 4 nu se află în primul set.
Observați că atunci când A este un subset corespunzător al lui B, atunci este, de asemenea, un subset al lui B.
Chiar mai multă notare
Când spunem că A este un subset al lui B, scriem A ![]() B.
B.
Sau noi poate spune că A nu este un subset al lui B de A ![]() B („A nu este un subset al lui B”)
B („A nu este un subset al lui B”)
Când vorbim despre subseturi adecvate, scoatem linia dedesubt și astfel devine A ![]() B sau dacă vrem să spunem opusul, A
B sau dacă vrem să spunem opusul, A ![]() B.
B.
Set gol (sau nul)
Acesta este probabil cel mai ciudat lucru despre seturi.

De exemplu, gândiți-vă la setul de taste de pian de pe o chitară.
„Dar așteptați!” spuneți: „Nu există taste de pian pe un chitară! „
Și ai dreptate. Este un set fără elemente.
Acesta este cunoscut sub numele de Set gol (sau set nul). Nu există elemente în el. Nici unul. Zero.
este reprezentat de ![]()
Sau de {} (un set fără elemente)
Unele alte exemple ale setului gol sunt setul a țărilor de la sud de polul sud.
Deci, ce este atât de ciudat la setul gol? Ei bine, acea parte vine în continuare.
Set gol și subseturi
Deci, să revenim la definiția noastră de subseturi. Avem un set A. Nu îl vom defini mai mult decât atât, ar putea fi orice set. Setul gol este un subset de A?
Revenind la definiția noastră de subseturi, dacă fiecare element din setul gol este, de asemenea, în A, atunci setul gol este un subset de A. Dar ce se întâmplă dacă nu aveți elemente?
Este nevoie de o introducere în logică pentru a înțelege acest lucru, dar această afirmație este una care este „vag” sau „trivial” adevărată.
Un mod bun de a vă gândi la este: nu putem găsi elemente din setul gol care nu sunt în A, deci trebuie să fie că toate elementele din setul gol sunt în A.
Deci, răspunsul la întrebarea pusă este un da răsunător.
Setul gol este un subset al fiecărui set, inclusiv setul gol în sine.
Ordinea
Nu, nu ordinea elementelor. În seturi nu contează în ce ordine sunt elementele.
Exemplu: {1,2,3,4} este același set ca {3,1,4,2}
Când spunem ordine în seturi ne referim la dimensiunea setului.
Un alt nume (mai bun) pentru acesta este cardinalitatea.
Un set finit are ordine finită (sau cardinalitate). Un set infinit are o ordine infinită (sau cardinalitate).
Pentru seturile finite ordinea (sau cardinalitatea) este numărul de elemente.
Exemplu: {10, 20, 30, 40} are o ordine de 4.
Pentru mulțimi infinite, tot ce putem spune este că ordinea este infinită. În mod ciudat, putem spune cu seturi că unele infinități sunt mai mari decât altele, dar acesta este un subiect mai avansat în seturi.
Arg! Nu mai multă notație!
Nu, glumesc. Gata cu notația.
de
și