Inlärningsmål
- Ange de Broglie vågekvationen.
- Använd denna ekvation för att beräkna våglängden för ett rörligt objekt.
Beyond Bohr’s Model
Bohrs modell av atomen var värdefull för att visa hur elektroner kunde absorbera och släppa energi och hur atomemissionsspektra skapades. Modellen förklarade dock inte riktigt varför elektroner bara borde existera i fasta cirkulära banor snarare än att kunna existera i ett obegränsat antal banor, alla med olika energier. För att förklara varför atomenergitillstånd kvantiseras, behövde forskare ompröva hur de betraktade elektronens natur och dess rörelse.
Plancks undersökning av emissionsspektra av heta föremål och de efterföljande studierna av den fotoelektriska effekten hade visat att ljus var kapabelt att bete sig både som en våg och som en partikel. Det verkade rimligt att undra om elektroner också kunde ha dubbla vågpartiklar. År 1924 härledde den franska forskaren Louis de Broglie (1892–1987) en ekvation som beskrev vågens natur hos varje partikel. Särskilt ges våglängden (λ) för varje rörligt objekt av:
\ displaystyle \ lambda = \ frac {h} {mv}
I denna ekvation är h Plancks konstant , m är partikelns massa i kg, och v är partikelns hastighet i m / s. Problemet nedan visar hur man beräknar elektronens våglängd.
Om vi skulle beräkna våglängden för en 0.145 kg baseball som kastades med en hastighet av 40 m / s, skulle vi komma med en extremt kort våglängd i storleksordningen 10−34 m. Denna våglängd är omöjlig att upptäcka även med avancerad vetenskaplig utrustning. Faktum är att medan alla objekt rör sig med våglik rörelse märker vi det aldrig eftersom våglängderna är alldeles för korta. Å andra sidan är partiklar med mätbara våglängder alla mycket små. Emellertid visade sig elektronens vågkaraktär vara en nyckelutveckling i en ny förståelse av elektronens natur. En elektron som är begränsad till ett visst utrymme runt en atoms kärna kan bara röra sig runt den atomen på ett sådant sätt att dess elektronvåg ”passar” atomens storlek korrekt. Detta innebär att frekvensen hos elektronvågorna kvantiseras. Baserat på E = hv-ekvationen betyder de kvantiserade frekvenserna att elektroner bara kan existera i en atom vid specifika energier, som Bohr tidigare hade teoretiserat.
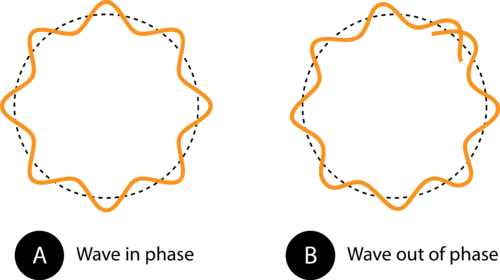
Figur 1. Banans omkrets i (A) gör att elektronvågen passar perfekt in i banan. Detta är en tillåten krets. I (B) gör elektronvågen inte passar ordentligt in i banan, så den här banan är inte tillåten.
Sammanfattning
- DeBroglie-vågekvationerna möjliggör beräkning av våglängden för varje rörelse objekt.
- När elektronens hastighet minskar ökar dess våglängd.
Övning
Använd länken nedan för att öva beräkningar med deBroglie-vågekvationen:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Granskning
- Vad förklarade inte Bohr-modellen?
- Ange deBroglie-vågekvationen.
- Vad händer när elektronens hastighet minskar?