Příklad: Náhodná čísla
Předpokládejme, že uvažujeme reálná čísla náhodně vybraná mezi 0 a 1, pro která zaznamenáváme \ (X_1 \), náhodné číslo zkráceno na jedno desetinné místo. Například číslo 0,07491234008 se zaznamená jako 0,0 (protože první desetinné místo je nula). To znamená, že nejsme zaokrouhlování, ale zkrácení. Pokud mechanismus generující tato čísla nemá preference pro žádnou pozici v intervalu \ ((0,1) \), pak rozdělení čísel, která získáme, bude takové, že
\
Toto je diskrétní náhoda proměnná se stejnou pravděpodobností pro každý z deseti možných výsledků.
\
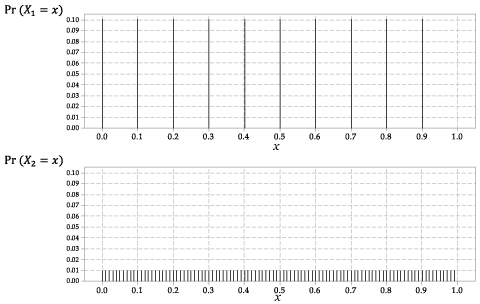
Distribuce \ (X_1 \) a \ (X_2 \) jsou znázorněny na obrázku 2.
Podrobný popis
Obrázek 2: Pravděpodobnostní funkce \ (p_ {X_1} (x) \) pro \ (X_1 \) a \ (p_ {X_2} (x) \) pro \ (X_2 \).
Excel má funkci, která vytváří reálná čísla mezi 0 a 1, zvolená tak, aby v intervalu nebyla preferována žádná poloha \ ( (0,1) \). Pokud do buňky zadáte \ (\ sf \ text {= RAND ()} \) a stisknete klávesu Return, získáte takové číslo. Zvyšte počet desetinných míst zobrazených v buňce. Pokračujte, dokud na konci čísla nedostanete hodně nul; možná budete muset zvětšit velikost buňky. Vaše tabulka by měla vypadat jako na obrázku 3, i když se konkrétní číslo samozřejmě bude lišit… koneckonců je to náhodné!
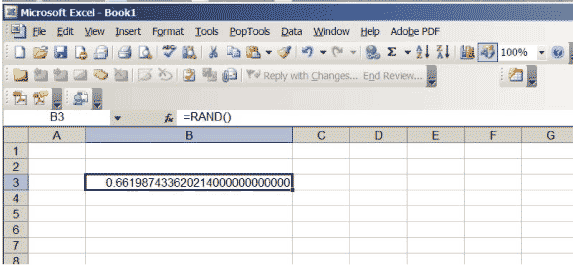
Obrázek 3: Tabulka aplikace Excel s náhodným číslem od 0 do 1.
Pokud v tomto okamžiku opakovaně stisknete klávesu „F9“, zobrazí se posloupnost náhodných čísel, vše mezi 0 a 1. Z jejich prozkoumání se zdá, že Excel ve skutečnosti vytváří pozorování na náhodné proměnné \ (X_ {15} \), prvních 15 desetinných míst čísla. Takže pravděpodobnost výskytu konkrétního jednoho z těchto čísel je \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0,3 \ leq X_1 < 0,4) & = \ Pr (X_1 = 0,3) = 0,1, \\\\ \ Pr (0,3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0,30) + \ Pr (X_2 = 0,31) + \ dots + \ Pr (X_2 = 0,39) \\\\ & = 10 \ krát 0,01 = 0,1, \\\\ \ Pr (0,3 \ leq X_3 < 0,4) & = 10 ^ 2 \ krát 10 ^ {- 3} = 0,1, \\\\ \ Pr (0,3 \ leq X_4 < 0,4) & = 10 ^ 3 \ krát 10 ^ {- 4} = 0,1, \\\\ & \ vdots \\\\ \ Pr (0,3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ krát 10 ^ {- k} = 0,1, \\\\ & \ vdots \ end {align *}
Jak děláme distribuci jemnější a jemnější, s více a více možnými diskrétními hodnotami, pravděpodobnost, že některá z těchto diskrétních náhodných proměnných leží v intervalu \ (
Například \ (\ Pr (0,3 \ leq U \ leq 0,4) = 0,4 – 0,3 = 0,1 \).
CDF této náhodné proměnné, \ (F_U (u) \), je tedy velmi jednoduchý. Je to
\
Následující obrázek ukazuje graf kumulativní distribuční funkce \ (U \).
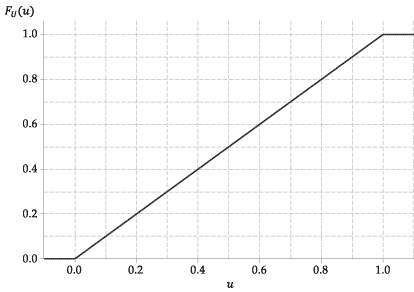
Obrázek 4: Kumulativní distribuční funkce \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Možná máte si všiml rozdílu v tom, jak se v kontinuálním případě zacházelo s intervalem mezi 0,3 a 0,4, ve srovnání s diskrétními případy. Ve všech diskrétních případech byly vyloučeny horní limity \ (0,4; 0,40; 0,400; \ tečky \), zatímco pro spojitou náhodnou proměnnou je zahrnuta. Kdykoli máme co do činění s diskrétními náhodnými proměnnými, záleží na tom, zda je nerovnost přísná nebo ne, a je třeba opatrnosti. Například
\ \