Esempio: numeri casuali
Supponiamo di considerare numeri reali scelti a caso tra 0 e 1, per i quali registriamo \ (X_1 \), il numero casuale troncato a una cifra decimale. Ad esempio, il numero 0,07491234008 viene registrato come 0,0 (poiché la prima cifra decimale è zero). Nota che questo significa che non stiamo arrotondando, ma troncando. Se il meccanismo che genera questi numeri non ha alcuna preferenza per alcuna posizione nell’intervallo \ ((0,1) \), la distribuzione dei numeri che otteniamo sarà tale che
\
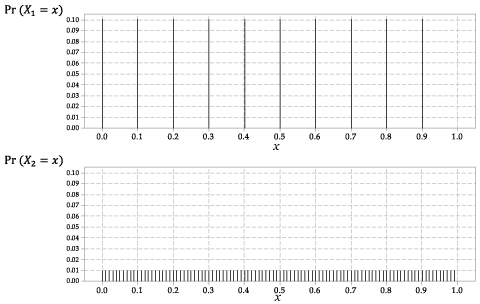
Questo è un discreto casuale variabile, con la stessa probabilità per ciascuno dei dieci possibili risultati.
\
Le distribuzioni di \ (X_1 \) e \ (X_2 \) sono mostrate nella figura 2.
Descrizione dettagliata
Figura 2: Le funzioni di probabilità \ (p_ {X_1} (x) \) per \ (X_1 \) e \ (p_ {X_2} (x) \) per \ (X_2 \).
Excel ha una funzione che produce numeri reali tra 0 e 1, scelti in modo che non ci sia preferenza per alcuna posizione nell’intervallo \ ( (0,1) \). Se inserisci \ (\ sf \ text {= RAND ()} \) in una cella e premi Invio, otterrai tale numero. Aumenta il numero di cifre decimali mostrato nella cella. Continua finché non ottieni molti zeri alla fine del numero; potrebbe essere necessario aumentare le dimensioni della cella. Il tuo foglio di lavoro dovrebbe assomigliare alla figura 3, anche se ovviamente il numero specifico sarà diverso … dopotutto è casuale!
Figura 3: un foglio di calcolo Excel con un numero casuale compreso tra 0 e 1.
Se premi ripetutamente il tasto “F9” a questo punto, vedrai una sequenza di numeri casuali, tutti compresi tra 0 e 1. Dall’esame di questi, sembra che Excel produca effettivamente osservazioni sulla variabile casuale \ (X_ {15} \), le prime 15 cifre decimali del numero. Quindi la possibilità che uno specifico di questi numeri si verifichi è \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ \ Pr (0.3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0.30) + \ Pr (X_2 = 0.31) + \ dots + \ Pr (X_2 = 0.39) \\\\ & = 10 \ times 0,01 = 0,1, \\\\ \ Pr (0,3 \ leq X_3 < 0,4) & = 10 ^ 2 \ times 10 ^ {- 3} = 0,1, \\\\ \ Pr (0,3 \ leq X_4 < 0,4) & = 10 ^ 3 \ volte 10 ^ {- 4} = 0,1, \\\\ & \ vdots \\\\ \ Pr (0,3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ times 10 ^ {- k} = 0.1, \\\\ & \ vdots \ end {align *}
Poiché rendiamo la distribuzione sempre più fine, con un numero sempre maggiore di valori discreti possibili, la probabilità che una qualsiasi di queste variabili casuali discrete si trovi nell’intervallo \ (
Ad esempio, \ (\ Pr (0.3 \ leq U \ leq 0.4) = 0.4 – 0.3 = 0.1 \).
Il cdf di questa variabile casuale, \ (F_U (u) \), è quindi molto semplice. È
\
La figura seguente mostra il grafico della funzione di distribuzione cumulativa di \ (U \).
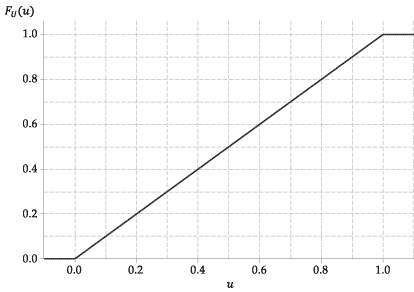
Figura 4: la funzione di distribuzione cumulativa di \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Potresti avere ho notato una differenza nel modo in cui è stato trattato l’intervallo tra 0,3 e 0,4 nel caso continuo, rispetto ai casi discreti. In tutti i casi discreti, i limiti superiori \ (0.4, 0.40, 0.400, \ dots \) sono stati esclusi, mentre per la variabile casuale continua è incluso. Ogni volta che abbiamo a che fare con variabili casuali discrete, spesso importa se la disuguaglianza è rigida o meno ed è necessaria attenzione. Ad esempio,
\ \