Ejemplo: números aleatorios
Supongamos que consideramos números reales elegidos aleatoriamente entre 0 y 1, para los cuales registramos \ (X_1 \), el número aleatorio truncado a un decimal. Por ejemplo, el número 0.07491234008 se registra como 0.0 (ya que el primer lugar decimal es cero). Tenga en cuenta que esto significa que no estamos redondeando, sino truncando. Si el mecanismo que genera estos números no tiene preferencia por ninguna posición en el intervalo \ ((0,1) \), entonces la distribución de los números que obtenemos será tal que
\
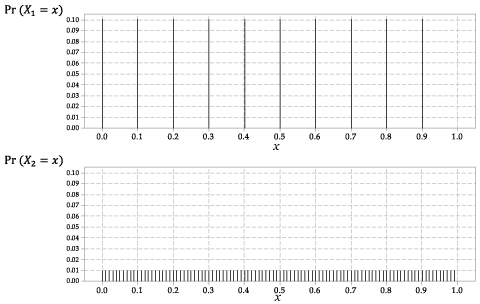
Este es un discreto aleatorio variable, con la misma probabilidad para cada uno de los diez resultados posibles.
\
Las distribuciones de \ (X_1 \) y \ (X_2 \) se muestran en la figura 2.
Descripción detallada
Figura 2: Las funciones de probabilidad \ (p_ {X_1} (x) \) para \ (X_1 \) y \ (p_ {X_2} (x) \) para \ (X_2 \).
Excel tiene una función que produce números reales entre 0 y 1, elegidos para que no haya preferencia por ninguna posición en el intervalo \ ( (0,1) \). Si ingresa \ (\ sf \ text {= RAND ()} \) en una celda y presiona regresar, obtendrá ese número. Aumente el número de lugares decimales que se muestran en la celda. Continúe hasta que obtenga muchos ceros al final del número; es posible que deba aumentar el tamaño de la celda. Su hoja de cálculo debe verse como la figura 3, aunque, por supuesto, el número específico será diferente … ¡es aleatorio, después de todo!
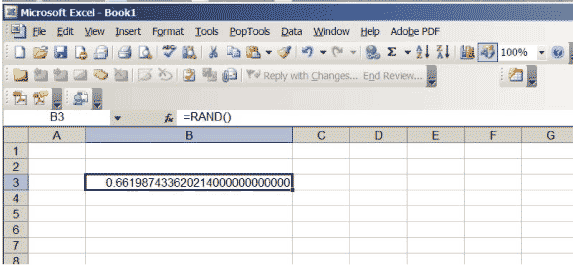
Figura 3: Una hoja de cálculo de Excel con un número aleatorio entre 0 y 1.
Si presiona la tecla «F9» repetidamente en este punto, verá una secuencia de números aleatorios, todos entre 0 y 1. Al examinarlos, parece que Excel en realidad produce observaciones sobre la variable aleatoria \ (X_ {15} \), los primeros 15 lugares decimales del número. Entonces, la probabilidad de que ocurra alguno de estos números es \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ \ Pr (0.3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0.30) + \ Pr (X_2 = 0.31) + \ dots + \ Pr (X_2 = 0.39) \\\\ & = 10 \ times 0.01 = 0.1, \\\\ \ Pr (0.3 \ leq X_3 < 0.4) & = 10 ^ 2 \ times 10 ^ {- 3} = 0.1, \\\\ \ Pr (0.3 \ leq X_4 < 0.4) & = 10 ^ 3 \ times 10 ^ {- 4} = 0.1, \\\\ & \ vdots \\\\ \ Pr (0.3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ times 10 ^ {- k} = 0.1, \\\\ & \ vdots \ end {align *}
A medida que hacemos la distribución más y más fina, con más y más valores discretos posibles, la probabilidad de que cualquiera de estas variables aleatorias discretas se encuentre en el intervalo \ (
Por ejemplo, \ (\ Pr (0.3 \ leq U \ leq 0.4) = 0.4 – 0.3 = 0.1 \).
El CDF de esta variable aleatoria, \ (F_U (u) \), es por tanto muy simple. Es
\
La siguiente figura muestra el gráfico de la función de distribución acumulativa de \ (U \).
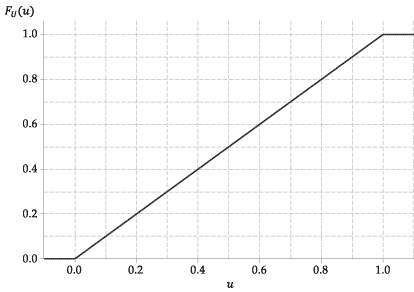
Figura 4: La función de distribución acumulativa de \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Es posible que haya notó una diferencia en cómo se trató el intervalo entre 0.3 y 0.4 en el caso continuo, en comparación con los casos discretos. En todos los casos discretos, se excluyeron los límites superiores \ (0.4, 0.40, 0.400, \ puntos \), mientras que para la variable aleatoria continua se incluye. Siempre que se trate de variables aleatorias discretas, a menudo importa si la desigualdad es estricta o no, y es necesario tener cuidado. Por ejemplo,
\ \