Læringsmål
- Angiv de Broglie-bølgeligning.
- Brug denne ligning til at beregne bølgelængden af et bevægeligt objekt.
Beyond Bohr’s Model
Bohrs model af atomet var værdifuldt til at demonstrere, hvordan elektroner var i stand til at absorbere og frigive energi, og hvordan atomemissionsspektre blev oprettet. Imidlertid forklarede modellen ikke rigtig, hvorfor elektroner kun skulle eksistere i faste cirkulære baner snarere end at være i stand til at eksistere i et ubegrænset antal baner, alle med forskellige energier. For at forklare, hvorfor atomare energitilstande kvantificeres, var forskere nødt til at genoverveje den måde, hvorpå de så på elektronens natur og dens bevægelse.
Plancks undersøgelse af emissionsspektre af varme genstande og de efterfølgende undersøgelser af den fotoelektriske effekt havde bevist, at lys var i stand til at opføre sig både som en bølge og som en partikel. Det syntes rimeligt at spekulere på, om elektroner også kunne have en dobbeltbølge-partikelkarakter. I 1924 afledte den franske videnskabsmand Louis de Broglie (1892–1987) en ligning, der beskrev bølgekarakteren for enhver partikel. Især bølgelængden (λ) for ethvert bevægeligt objekt er givet ved:
\ displaystyle \ lambda = \ frac {h} {mv}
I denne ligning er h Plancks konstant , m er massen af partiklen i kg, og v er partikelhastigheden i m / s. Problemet nedenfor viser, hvordan man beregner elektronens bølgelængde.
Hvis vi skulle beregne bølgelængden for en 0,125 kg baseball, der blev kastet med en hastighed på 40 m / s, ville vi komme op med en ekstremt kort bølgelængde i størrelsesordenen 10−34 m. Denne bølgelængde er umulig at detektere selv med avanceret videnskabeligt udstyr. Faktisk, mens alle objekter bevæger sig med bølgelignende bevægelse, bemærker vi det aldrig, fordi bølgelængderne er alt for korte. På den anden side er partikler med målbare bølgelængder alle meget små. Imidlertid viste sig bølgenaturen af elektronen at være en nøgleudvikling i en ny forståelse af elektronens natur. En elektron, der er begrænset til et bestemt rum omkring atomets kerne, kan kun bevæge sig rundt om det atom på en sådan måde, at dets elektronbølge “passer” til atomets størrelse korrekt. Dette betyder, at frekvenserne af elektronbølger kvantiseres. Baseret på E = hv-ligningen betyder de kvantiserede frekvenser, at elektroner kun kan eksistere i et atom ved specifikke energier, som Bohr tidligere havde teoretiseret.
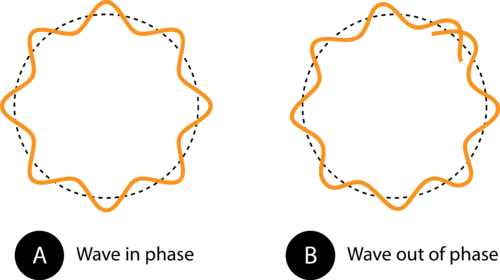
Figur 1. Omkredsen af banen i (A) gør det muligt for elektronbølgen at passe perfekt ind i banen. Dette er en tilladt bane. I (B) gør elektronbølgen ikke passer ordentligt ind i kredsløbet, så denne bane er ikke tilladt.
Resumé
- DeBroglie-bølgeligningerne tillader beregning af bølgelængden for enhver bevægelse objekt.
- Når elektronens hastighed falder, øges dens bølgelængde.
Øvelse
Brug linket nedenfor for at øve beregninger ved hjælp af deBroglie bølgeligning:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Review
- Hvad forklarede Bohr-modellen ikke?
- Angiv deBroglie-bølgeligning.
- Hvad sker der, når elektronens hastighed falder?