Objetivos de aprendizaje
- Indique la ecuación de onda de De Broglie.
- Utilice esta ecuación para calcular la longitud de onda de un objeto en movimiento.
Más allá del modelo de Bohr
El modelo de Bohr del átomo fue valioso para demostrar cómo los electrones fueron capaces de absorber y liberar energía y cómo se crearon los espectros de emisión atómica. Sin embargo, el modelo no explicaba realmente por qué los electrones deberían existir solo en órbitas circulares fijas en lugar de poder existir en un número ilimitado de órbitas, todas con diferentes energías. Para explicar por qué se cuantifican los estados de energía atómica, los científicos necesitaban repensar la forma en que veían la naturaleza del electrón y su movimiento.
La investigación de Planck sobre los espectros de emisión de objetos calientes y los estudios posteriores sobre el efecto fotoeléctrico habían demostrado que la luz era capaz de comportarse tanto como onda como como partícula. Parecía razonable preguntarse si los electrones también podrían tener una naturaleza de partícula de onda dual. En 1924, el científico francés Louis de Broglie (1892-1987) derivó una ecuación que describía la naturaleza ondulatoria de cualquier partícula. En particular, la longitud de onda (λ) de cualquier objeto en movimiento viene dada por:
\ displaystyle \ lambda = \ frac {h} {mv}
En esta ecuación, h es la constante de Planck , m es la masa de la partícula en kg, y v es la velocidad de la partícula en m / s. El siguiente problema muestra cómo calcular la longitud de onda del electrón.
Si tuviéramos que calcular la longitud de onda de una pelota de béisbol de 0.145 kg lanzada a una velocidad de 40 m / s, obtendríamos una longitud de onda del orden de 10−34 m. Esta longitud de onda es imposible de detectar incluso con equipos científicos avanzados. De hecho, aunque todos los objetos se mueven con un movimiento ondulatorio, nunca lo notamos porque las longitudes de onda son demasiado cortas. Por otro lado, las partículas con longitudes de onda medibles son todas muy pequeñas. Sin embargo, la naturaleza ondulatoria del electrón resultó ser un avance clave en una nueva comprensión de la naturaleza del electrón. Un electrón que está confinado a un espacio particular alrededor del núcleo de un átomo solo puede moverse alrededor de ese átomo de tal manera que su onda de electrones «se ajuste» correctamente al tamaño del átomo, lo que significa que las frecuencias de las ondas de electrones están cuantificadas. Según la ecuación E = hv, las frecuencias cuantificadas significan que los electrones solo pueden existir en un átomo a energías específicas, como Bohr había teorizado previamente.
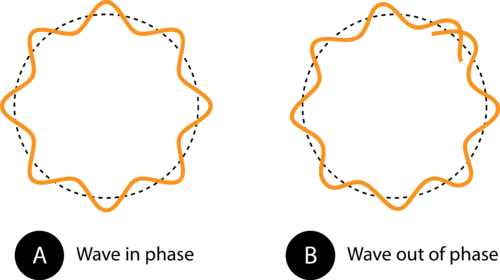
Figura 1. La circunferencia de la órbita en (A) permite que la onda de electrones encaje perfectamente en la órbita. Esta es una órbita permitida. En (B), la onda de electrones no encajar correctamente en la órbita, por lo que esta órbita no está permitida.
Resumen
- Las ecuaciones de onda de DeBroglie permiten el cálculo de la longitud de onda de cualquier movimiento objeto.
- A medida que la velocidad del electrón disminuye, su longitud de onda aumenta.
Practica
Use el enlace a continuación para practicar cálculos usando la ecuación de onda de DeBroglie:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Revisar
- ¿Qué ¿No explicó el modelo de Bohr?
- Exprese la ecuación de onda de DeBroglie.
- ¿Qué sucede cuando la velocidad del electrón disminuye?