Esimerkki: Satunnaisluvut
Oletetaan, että tarkastellaan satunnaisesti välillä 0 – 1 valittuja reaalilukuja, joille tallennamme \ (X_1 \), satunnaisluku lyhennetty yhden desimaalin tarkkuudella. Esimerkiksi numero 0,07491234008 kirjataan 0,0: ksi (koska ensimmäinen desimaali on nolla). Huomaa, että tämä tarkoittaa, että emme pyöristää, vaan katkaisemme. Jos nämä luvut generoivalla mekanismilla ei ole etusijaa millekään sijalle välissä \ ((0,1) \), niin saamiemme numeroiden jakauma on sellainen, että
\
Tämä on erillinen satunnainen muuttuja, samalla todennäköisyydellä kullekin kymmenelle mahdolliselle tulokselle.
\
\ (X_1 \) ja \ (X_2 \) jakaumat on esitetty kuvassa 2.
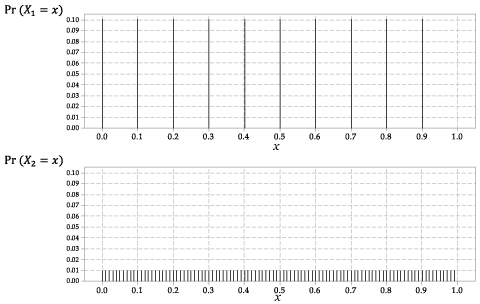
Yksityiskohtainen kuvaus
Kuva 2: Todennäköisyysfunktiot \ (p_ {X_1} (x) \) kohteille \ (X_1 \) ja \ (p_ {X_2} (x) \) \ (X_2 \).
Excelissä on toiminto, joka tuottaa reaalilukuja välillä 0 ja 1, valittu siten, että aikavälillä ei aseteta etusijalle mitään sijaintia \ ( (0,1) \). Jos syötät soluun \ (\ sf \ text {= RAND ()} \) ja painat return, saat tällaisen numeron. Lisää solussa näkyvien desimaalien määrää. Jatka, kunnes saat paljon nollia numeron loppuun; saatat joutua kasvattamaan solun kokoa. Laskentataulukon tulisi näyttää kuvalta 3, vaikka tietysti tietty numero on erilainen … se on loppujen lopuksi satunnainen!
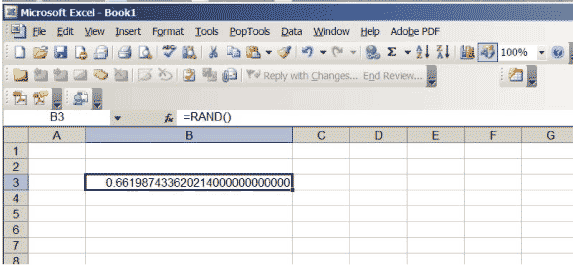
Kuva 3: Excel-laskentataulukko, jonka satunnaisluku on välillä 0 ja 1.
Jos painat näppäintä ”F9” toistuvasti tässä vaiheessa, näet satunnaislukujen sarjan, jotka kaikki ovat välillä 0 ja 1. 1. Näitä tutkimalla käy ilmi, että Excel tuottaa todellakin havaintoja satunnaismuuttujaan \ (X_ {15} \), joka on luvun ensimmäiset 15 desimaalia. Joten minkä tahansa tietyn näistä luvuista voi esiintyä \ (10 ^ {- 15} \).
\ begin {tasaa *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ Pr (0.3 \ leq X_2 < 0,4) & = \ Pr (X_2 = 0,30) + \ Pr (X_2 = 0,31) + \ pistettä + \ Pr (X_2 = 0,39) \\\\ & = 10 \ kertaa 0,01 = 0,1, \\\\ \ Pr (0,3 \ leq X_3 < 0,4) & = 10 ^ 2 \ kertaa 10 ^ {- 3} = 0,1, \\\\ Pr (0,3 \ leq X_4 < 0,4) & = 10 ^ 3 \ kertaa 10 ^ {- 4} = 0,1, \\\\ & \ vdots \\\\ Pr (0,3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ kertaa 10 ^ {- k} = 0.1, \\\\ & \ vdots \ end {align *}
Kun teemme jakelusta hienomman ja hienomman, yhä useammilla mahdollisilla erillisillä arvoilla, todennäköisyys, että jokin näistä erillisistä satunnaismuuttujista on välissä \ (
Esimerkiksi \ (\ Pr (0,3 \ leq U \ leq 0,4) = 0,4 – 0,3 = 0,1 \).
Tämän satunnaismuuttujan \ (F_U (u) \), on siksi hyvin yksinkertainen. Se on
\
Seuraava kuva näyttää kaavion \ (U \) kumulatiivisesta jakelutoiminnosta.
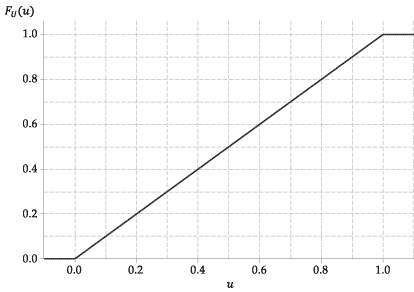
Kuva 4: \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \) kumulatiivinen jakelutoiminto.
Sinulla saattaa olla huomasi eron siinä, miten 0,3 ja 0,4 välistä väliä kohdeltiin jatkuvassa tapauksessa verrattuna erillisiin tapauksiin. Kaikissa erillisissä tapauksissa ylärajat \ (0,4, 0,40, 0,400, \ pisteet \) suljettiin pois, kun taas jatkuvalle satunnaismuuttujalle se sisältyy. Aina kun on kyse erillisistä satunnaismuuttujista, on usein merkitystä sillä, onko epätasa-arvo tiukka vai ei, ja hoitoa tarvitaan. Esimerkiksi
\ \