Analyse coût-volume-profit

L’analyse Coût-Volume-Profit (CVP) est une technique de comptabilité managériale qui étudie l’effet du volume des ventes et des coûts des produits sur le bénéfice d’exploitation d’une entreprise. Il montre comment le bénéfice d’exploitation est affecté par les variations des coûts variables, des coûts fixes, du prix de vente unitaire et du mix des ventes de deux produits ou plus.

L’analyse CVP concerne l’identification des coûts fixes d’une entreprise , son coût unitaire variable, le prix de son produit et en utilisant ces données pour élaborer les mesures suivantes:

• Marge de contribution: la différence entre les revenus totaux d’une entreprise et les coûts variables totaux. Il s’agit du montant que les ventes contribuent aux coûts fixes et aux bénéfices.
• Marge de contribution par unité: la différence entre le prix de vente et le coût variable par unité.
• Ratio de marge de contribution: le ratio de marge de contribution au chiffre d’affaires total.
• Seuil de rentabilité: le volume des ventes (en unités et en dollars) auquel l’entreprise ne fait aucune perte ni ne réalise de profit.
• Ventes à revenu cible: le niveau de ventes nécessaire pour atteindre un revenu cible.
• Marge de sécurité: pourcentage (ou dollars) par lequel le volume des ventes d’une entreprise dépasse son seuil de rentabilité.

L’entrée la plus critique dans l’analyse CVP est la relation entre les différents coûts et le volume, c’est-à-dire la catégorisation des coûts en catégories fixes et variables.

Equation d’analyse CVP

La relation fondamentale coût-volume-profit peut être dérivée de l’équation de profit:

Profit = Revenu – Coûts fixes – Coûts variables

Lorsque le profit est PR, le revenu est égal au produit du prix par unité P et du volume des ventes en unités Q , les coûts fixes FC sont constants et les coûts variables totaux sont égaux au produit des unités vendues Q et du coût variable par unité V, l’équation suivante est une représentation plus élaborée des relations CVP:

PR = Q × P – Q × V – FC

C’est l’équation la plus fondamentale qui peut être utilisée pour travailler de nombreux nombres CVP.

Pour la pause -même point, nous devons définir PR ad 0 et résoudre pour Q et nous obtenons:

Seuil de rentabilité Q = FC ÷ (P – V)

Cela montre que la rupture- Le point pair peut être calculé en divisant le coût fixe par la marge de contribution par unité.

Approche par équation de marge de contribution

L’équation CVP discutée ci-dessus peut également être exprimée en termes de marge de contribution du produit:

PR = Q × P – Q × V – FC

PR = Q × (P – V) – FC

(P – V) dans l’équation ci-dessus, la marge de contribution par unité.

Graphe CVP

La relation CVP peut également être exprimée sous la forme d’un graphe appelé graphe CVP:

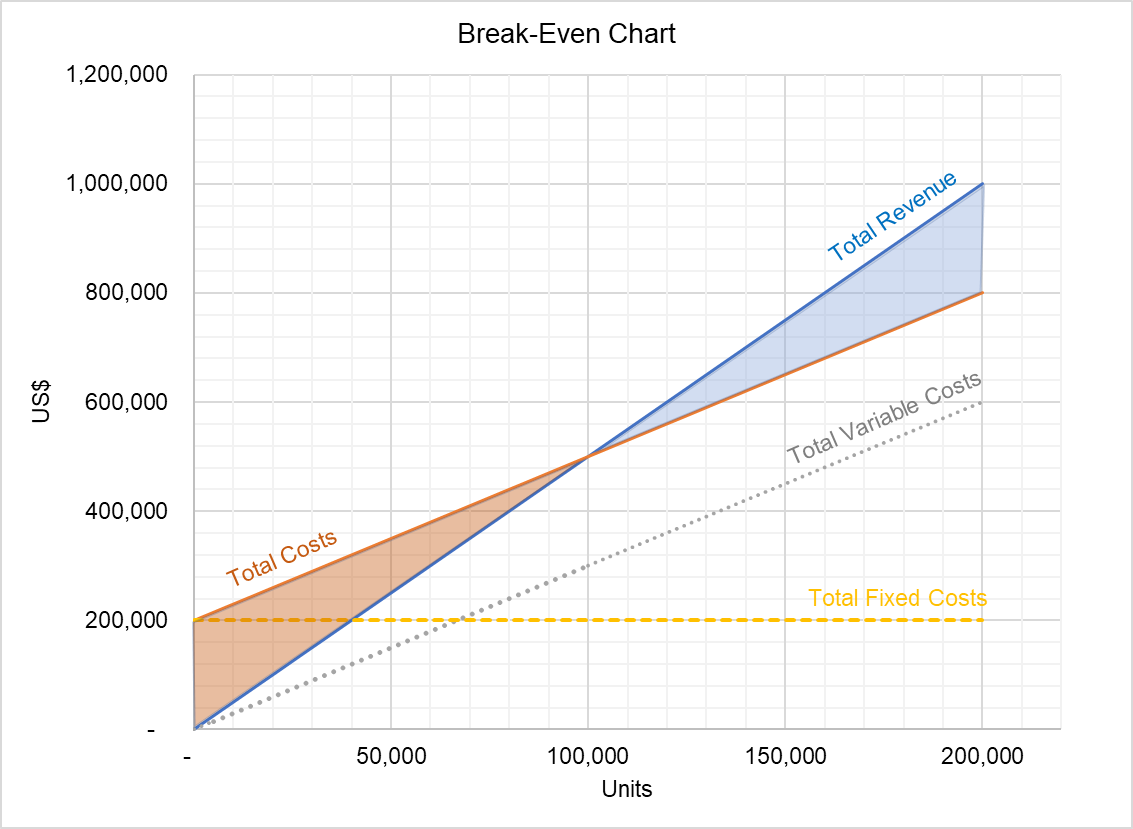
Le graphique ci-dessus montre la relation entre les revenus totaux et les coûts totaux. La zone entre les deux lignes sous le seuil de rentabilité représente les pertes et la zone au-dessus du seuil de rentabilité indique le volume du bénéfice total. Ce graphique peut être utilisé pour identifier le profit à différents niveaux de sortie.

Hypothèses d’analyse CVP

Même si l’analyse CVP est un outil de comptabilité de gestion utile, ses conclusions ne sont valables que lorsque les hypothèses suivantes hold:

• Tous les coûts peuvent être classés comme variables ou fixes. À cette fin, les coûts mixtes sont divisés en composants variables et fixes en utilisant des techniques telles que la méthode haut-bas, la méthode du nuage de points et l’analyse de régression.
• Le prix de vente par unité, le coût variable par unité et le coût fixe total sont constants . Cette hypothèse est problématique en raison de l’existence d’économies d’échelle, des rendements d’échelle croissants / décroissants et de l’effet de la courbe d’apprentissage.
• Tous les revenus et les coûts ont une relation linéaire avec le volume.
• Les ventes mélange d’une entreprise reste constant.

par Irfanullah Jan, ACCA et dernière modification le 2 octobre 2020