Qu’est-ce que l’écart type? | STDEV.P | STDEV.S | Variance
Cette page explique comment calculer l’écart type sur la base de la population entière à l’aide de la fonction STDEV.P dans Excel et comment estimer l’écart type sur la base d’un échantillon à l’aide de la fonction STDEV.S dans Excel.
Qu’est-ce que l’écart type?
L’écart type est un nombre qui vous indique à quel point les nombres sont éloignés de leur moyenne.
1. Par exemple, les nombres ci-dessous ont une moyenne (moyenne) de 10.
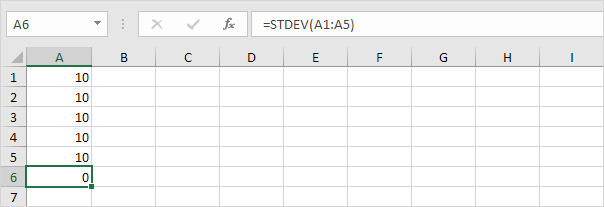
Explication: les nombres sont tous les mêmes qui signifie qu’il n’y a pas de variation. Par conséquent, les nombres ont un écart type de zéro. La fonction STDEV est une ancienne fonction. Microsoft Excel recommande d’utiliser la nouvelle fonction STEDV.S qui produit exactement le même résultat.
2. Les nombres ci-dessous ont également une moyenne (moyenne) de 10.
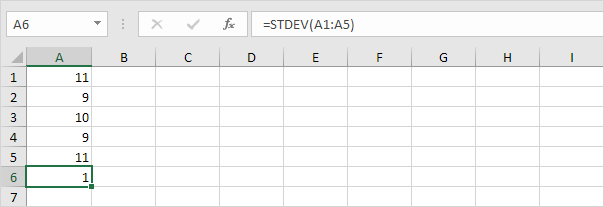
Explication: les nombres sont proches de la moyenne. Par conséquent, les nombres ont un faible écart type.
3. Les nombres ci-dessous ont également une moyenne (moyenne) de 10.
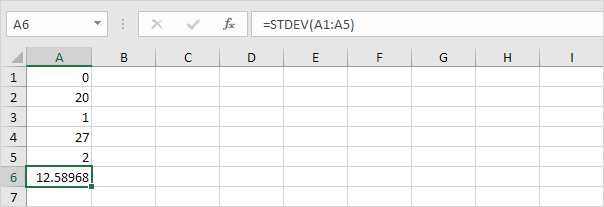
Explication: les nombres sont répartis. Par conséquent, les nombres ont un écart type élevé.
STDEV.P
La fonction STDEV.P (le P signifie Population) dans Excel calcule l’écart type sur la base de la population entière. Par exemple, vous « enseignez à un groupe de 5 étudiants. Vous avez les résultats des tests de tous les élèves. La population entière se compose de 5 points de données. La fonction STDEV.P utilise la formule suivante:
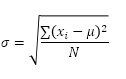
Dans cet exemple, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (moyenne), N = 5 (nombre de points de données).
1. Calculez la moyenne (μ).
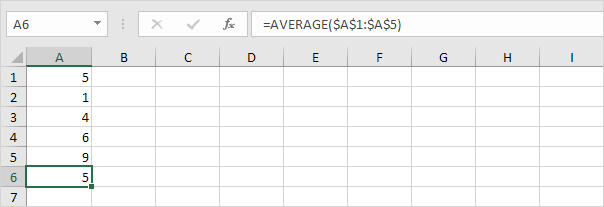
2. Pour chaque nombre, calculez la distance à la moyenne.
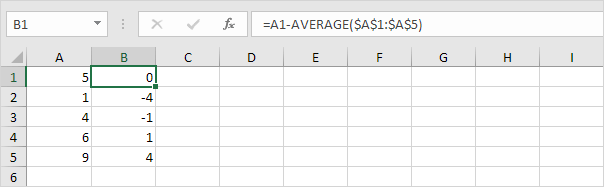
3. Pour chaque nombre, mettez cette distance au carré.
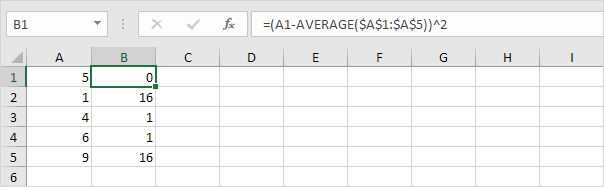
4. Additionnez (∑) ces valeurs.
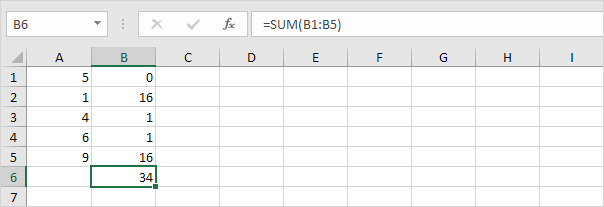
5. Divisez par le nombre de points de données (N = 5).
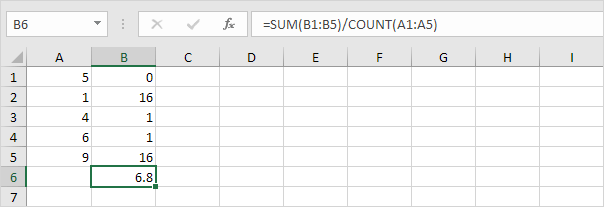
6. Prenez la racine carrée.
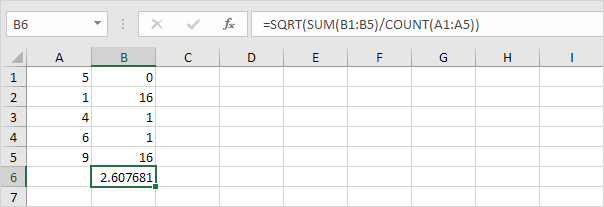
7. Heureusement, la fonction STDEV.P d’Excel peut exécuter toutes ces étapes pour vous.
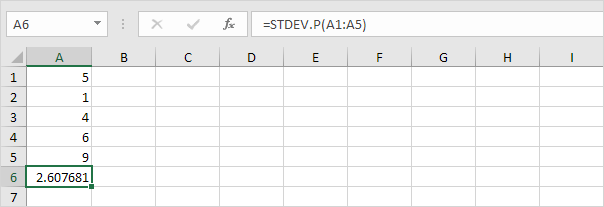
STDEV.S
La fonction STDEV.S (le S signifie Sample) dans Excel estime l’écart type sur la base d’un échantillon. Par exemple, vous « enseignez à un grand groupe d’élèves. Vous n’avez que les résultats de 5 élèves. La taille de l’échantillon est égale à 5. La fonction STDEV.S utilise la formule suivante:
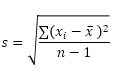
Dans cet exemple, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (mêmes nombres que ci-dessus), x̄ = 5 (échantillon moyenne), n = 5 (taille de l’échantillon).
1. Répétez les étapes 1 à 5 ci-dessus mais à l’étape 5, divisez par n-1 au lieu de N.
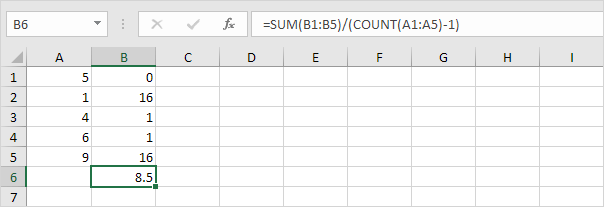
2. Prenez la racine carrée.
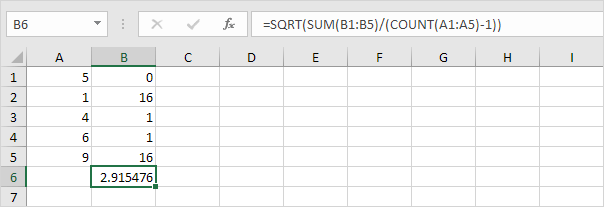
3. Heureusement, la fonction STDEV.S d’Excel peut exécuter toutes ces étapes pour vous.
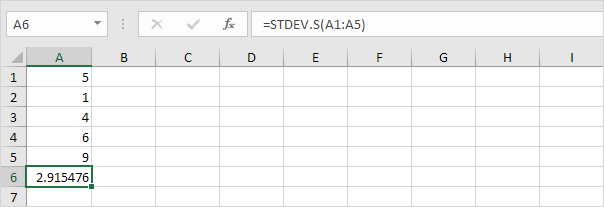
Remarque: pourquoi divisons-nous par n – 1 au lieu de par n lorsque nous estimons l’écart type sur la base d’un échantillon? La correction de Bessel indique que la division par n-1 au lieu de n donne une meilleure estimation de l’écart type.
Variance
La variance est le carré de l’écart type. C’est aussi simple que cela. Parfois, il est plus facile d’utiliser la variance pour résoudre des problèmes statistiques.
1. La fonction VAR.P ci-dessous calcule la variance en fonction de l’ensemble de la population.
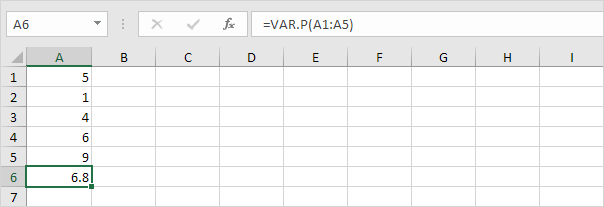
Remarque: vous connaissiez déjà cette réponse (voir étape 5 sous STDEV.P). Prenez la racine carrée de ce résultat pour trouver l’écart-type basé sur l’ensemble de la population.
2. La fonction VAR.S ci-dessous estime la variance en fonction d’un échantillon.
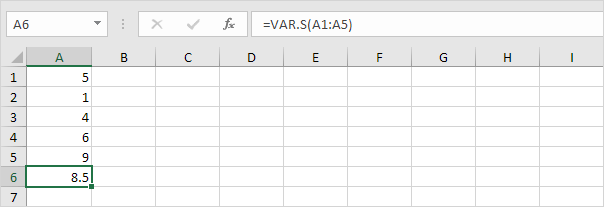
Remarque: vous connaissiez déjà cette réponse (voir étape 1 sous STDEV.S). Prenez la racine carrée de ce résultat pour trouver l’écart-type basé sur un échantillon.
3. VAR et VAR.S produisent exactement le même résultat.
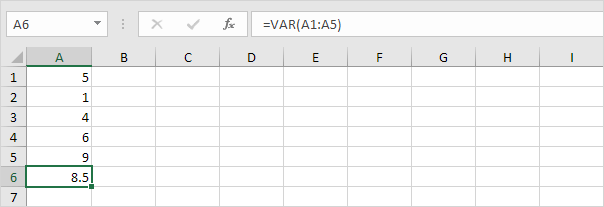
Remarque: Microsoft Excel recommande d’utiliser la nouvelle fonction VAR.S.