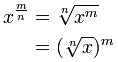Aussi appelés « radicaux » ou « exposants rationnels »
Exposants de nombres entiers
Tout d’abord, examinons le nombre entier exposants:

L’exposant d’un nombre indique combien de fois utiliser le nombre dans une multiplication.
Dans cet exemple: 82 = 8 × 8 = 64
Autre exemple: 53 = 5 × 5 × 5 = 125
Exposants fractionnaires
Mais que faire si l’exposant est une fraction?
|
Un exposant de 12 est en fait une racine carrée Un exposant de 13 est la racine cubique Un exposant de 14 est la 4ème racine Et ainsi de suite! |
 |
Pourquoi?
Voyons pourquoi dans un exemple.
Premièrement, les lois des exposants nous indiquent comment gérer les exposants lorsque nous multiplions:
Exemple: x2x2 = (xx) (xx) = xxxx = x4
Ce qui montre que x2x2 = x (2 + 2) = x4
Alors essayons cela avec des exposants fractionnaires:
Essayez une autre fraction
Essayons à nouveau, mais avec un exposant d’un quart (1/4):
Exemple:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Donc, 16¼ utilisé 4 fois dans une multiplication donne 16,
et donc 16¼ est un 4ème racine de 16
Règle générale
Cela a fonctionné pendant ½, ça a marché avec ¼, en fait ça marche généralement:
x1 / n = La n-ième racine de x
Nous pouvons donc trouver ceci:
| |
|
Exemple: Qu’est-ce que 271/3?
Réponse: 271/3 = ![]() 27 = 3
27 = 3
Et les fractions plus compliquées?
Qu’en est-il d’un exposant fractionnaire comme 43/2?
Cela veut dire vraiment faire un cube (3) et une racine carrée (1/2), dans n’importe quel ordre.
Laissez-moi vous expliquer.
Une fraction (comme m / n) peut être divisée en deux parties:
- une partie de nombre entier (m), et
- une fraction (1 / n) part
Donc, parce que m / n = m × (1 / n) nous pouvons faire ceci:
L’ordre n’a pas d’importance, donc cela fonctionne aussi pour m / n = (1 / n) × m:
Et nous obtenons ceci:
| |
|
Quelques exemples:
Exemple : Qu’est-ce que 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
ou
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
Dans les deux cas, on obtient le même résultat.
Exemple: Qu’est-ce que 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
ou
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
C’était certainement plus facile avec la deuxième manière!
Maintenant … Jouez avec le graphique!
Voyez avec quelle douceur la courbe change lorsque vous jouez avec les fractions dans cette animation, cela vous montre que cette idée d’exposants fractionnaires s’accorde bien:
Choses à essayer:
- Commencez par m = 1 et n = 1, puis augmentez lentement n pour que vous puissiez voir 1/2, 1/3 et 1/4
- Puis essayez m = 2 et faites glisser n de haut en bas pour voir des fractions comme 2/3 etc
- Maintenant, essayez de rendre l’exposant -1
- Essayez enfin d’augmenter m, puis de réduire n, puis de réduire m, puis d’augmenter n: la courbe doit tourner en rond