La conjecture de Poincaré et 6 autres théories mathématiques complexes ont été surnommées les problèmes du prix du millénaire par le Clay Mathematics Institute (CMI). Chaque problème a été décrit comme une « question classique importante qui a résisté à des solutions au fil des ans », la première personne à trouver une solution pour chaque gagnant de 1 000 000 $ grâce au CMI. Cependant, comme vous l’avez vu ci-dessus, résoudre ces problèmes n’est pas facile Un des problèmes est resté non résolu depuis sa formulation en 1859 par le mathématicien allemand Bernhard Riemann.
L’hypothèse de Riemann, du nom du mathématicien allemand susmentionné, est largement considérée comme le problème non résolu le plus important en mathématiques. Elle présente un grand intérêt pour la théorie des nombres car elle implique des résultats sur la distribution des nombres premiers, qui sont utilisés dans tout, de la biologie au chiffrement et à la mécanique quantique. Afin de comprendre l’hypothèse de Riemann, nous devons d’abord expliquer quelques clés concepts:
- Un nombre complexe est de la forme a + bi, où i est défini par i² = -1. Sous cette forme, la partie réelle d’un nombre complexe est a, et l’imaginaire une partie est bi.
- La fonction zêta de Riemann est une fonction d’une variable complexe (une fonction de nombres complexes) définie par l’équation suivante, où s est tout nombre complexe autre que 1, et dont les valeurs sont également complexes:
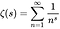
- Un « zéro » d’une fonction est un x tel que f (x) = 0
- Les « zéros triviaux » de la fonction zêta de Riemann sont tous les entiers négatifs pairs (-2, -4, -6,…)
- Les « zéros non triviaux »De la fonction zêta de Riemann sont toutes les autres valeurs de s pour lesquelles ζ (s) = 0 (ie. s n’est pas un entier pair négatif).
Maintenant que nous avons quelques définitions, nous pouvons aller de l’avant et énoncer l’hypothèse de Riemann:
La partie réelle de chaque zéro non trivial de la fonction zêta de Riemann est 1/2
Celui-ci (pour moi du moins) est beaucoup plus facile à comprendre que la conjecture de Poincaré et ne semble pas intuitivement très difficile. Cependant, cela ne semble pas non plus vouloir dire grand-chose. Vraiment, qui se soucie de savoir quand cette fonction aléatoire a une valeur de 0. Eh bien, sans surprise, beaucoup de mathématiciens le font, et pour une très bonne raison.
Certains nombres ont la propriété spéciale qu’ils ne peuvent pas être exprimés comme le produit de deux nombres plus petits (le produit étant la multiplication), ie. 2,3,5,7,11, etc. Connus sous le nom de nombres premiers, ils sont en un sens les nombres les plus simples que vous puissiez obtenir, formant les blocs de construction pour tous les autres nombres. Frustrant cependant, les nombres premiers ne semblent suivre aucun modèle. 3137 est un nombre premier, et le suivant n’est pas avant 3163, mais ensuite 3167 et 3169 se succèdent rapidement, tous étant premiers. En un mot, si vous trouvez un nombre premier, il n’y a aucun moyen de savoir où sera le prochain sans vérifier tous les nombres au fur et à mesure. Cependant, en utilisant le théorème des nombres premiers (PNT), vous pouvez trouver combien de nombres premiers il y a en dessous d’un certain seuil.
Le théorème des nombres premiers n’est qu’une estimation, avec des valeurs différentes donnant une probabilité différente d’être correct, mais jamais de certitude à 100%. Cependant, comprenez l’hypothèse que l’hypothèse de Reimann est vraie, vous pouvez créer une approximation mathématique combinant le théorème des nombres premiers et les zéros non triviaux de la fonction zêta de Riemann pour corriger les erreurs des composants internes, fournissant la « meilleure » borne pour le terme d’erreur dans le théorème des nombres premiers. S’il était possible de prouver complètement l’hypothèse de Reimann, cela donnerait au PNT la capacité de fournir des estimations incroyablement proches de la valeur réelle, ouvrant ainsi de nombreuses possibilités dans différentes branches des mathématiques. En fait, il existe de nombreuses hypothèses importantes selon lesquelles être avec «Si l’hypothèse de Riemann est vraie, alors…», donc résoudre ce problème validerait instantanément toutes les conjectures suivantes.