Oubliez tout ce que vous savez sur les nombres.
En fait, oubliez même que vous savez ce qu’est un nombre.
Ceci c’est là que les mathématiques commencent.
Au lieu des mathématiques avec des nombres, nous allons maintenant penser aux mathématiques avec des «choses».
Définition
Qu’est-ce que un ensemble? Eh bien, en termes simples, c’est une collection.
D’abord, nous spécifions une propriété commune parmi les « choses » (nous définissons ce mot plus tard) et ensuite nous rassemblons toutes les « choses » qui ont cette propriété commune.

Par exemple, les articles que vous portez: chapeau, chemise, veste, pantalon , et ainsi de suite.
Je suis sûr que vous pourriez en trouver au moins une centaine.
C’est ce qu’on appelle un ensemble.
|
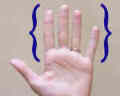
Ou un autre exemple est les types de doigts. Cet ensemble comprend l’index, le milieu, l’anneau et pinky. |
 |
Il s’agit donc simplement de choses regroupées avec une certaine propriété en commun.
Notation
Il y a une notation assez simple pour les ensembles. Nous listons simplement chaque élément (ou « membre ») séparé par une virgule, puis mettons des accolades autour du tout:

Les accolades {} sont parfois appelées « parenthèses » ou « accolades ».
Voici la notation des deux exemples précédents:
{chaussettes, chaussures, montres, chemises, …}
{index, milieu, anneau, pinky}
Remarquez comment le premier exemple a le « … » (trois points ensemble) .
Les trois points … sont appelés points de suspension et signifient « continuer ».
Cela signifie que le premier exemple continue. . pour l’infini.
(OK, il n’y a pas vraiment une quantité infinie de choses que vous pourriez porter, mais je ne suis pas tout à fait sûr de cela! Après une heure à penser à différentes choses, je « m toujours pas sûr. Alors disons simplement que c’est infini pour cet exemple.)
Donc:
Mais parfois le « … » peut être utilisé au milieu pour enregistrer écrire de longues listes:
Exemple: l’ensemble des lettres:
{a, b, c, .. ., x, y, z}
Dans ce cas, c’est un ensemble fini (il n’y a que 26 lettres, non?)
Ensembles numériques
Qu’est-ce que cela a à voir avec les mathématiques? Lorsque nous définissons un ensemble, il suffit de spécifier une caractéristique commune. Qui a dit que nous ne pouvions « pas le faire avec des nombres?
Et ainsi de suite. Nous pouvons proposer tous les types d’ensembles.
Nous pouvons également définir un ensemble par ses propriétés, comme {x | x > 0} qui signifie « l’ensemble de tous les x », tel que x est supérieur à 0 « , voir Notation Set-Builder pour en savoir plus.
Et nous pouvons avoir des ensembles de nombres qui n’ont pas de propriété commune, ils sont simplement définis de cette façon. Par exemple:
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203 }
Sont tous les ensembles que je viens de frapper au hasard sur mon clavier pour produire.
Pourquoi les ensembles sont-ils importants?
Les ensembles sont la propriété fondamentale des mathématiques. Maintenant, en guise d’avertissement, les décors, en eux-mêmes, semblent assez inutiles. Mais ce n’est que lorsque nous appliquons des ensembles dans différentes situations qu’ils deviennent la puissante composante des mathématiques qu’ils sont.
Les mathématiques peuvent devenir incroyablement compliquées assez rapidement. Théorie des graphes, algèbre abstraite, analyse réelle, complexe Analyse, algèbre linéaire, théorie des nombres et la liste est longue. Mais il y a une chose que tous ces éléments ont en commun: les ensembles.
Universal Set
 |
Au début, nous avons utilisé le mot «choses» entre guillemets. Nous l’appelons l’ensemble universel. C’est un ensemble qui contient tout. Eh bien, pas exactement tout. Tout ce qui concerne notre question. |
|
 |
Dans la théorie des nombres, l’ensemble universel est composé de tous les entiers, car la théorie des nombres est simplement le étude d’entiers. |
|
 |
Mais en calcul (également appelé analyse réelle), l’ensemble universel est presque toujours les nombres réels. |
|
 |
Et dans l’analyse complexe, vous l’avez deviné, l’ensemble universel est les nombres complexes. |
Encore plus de notation
 |
Quand on parle d’ensembles, il est assez courant d’utiliser des lettres majuscules pour représenter l’ensemble et des lettres minuscules pour représenter un élément de cet ensemble. Ainsi, par exemple, A est un ensemble et a est un élément nt dans A. Idem avec B et b, et C et c. |
Vous n’avez plus à écouter le standard , vous pouvez utiliser quelque chose comme m pour représenter un ensemble sans enfreindre aucune loi mathématique (attention, vous pouvez passer π ans en prison mathématique en divisant par 0), mais cette notation est assez agréable et facile à suivre, alors pourquoi pas?
De plus, quand nous disons qu’un élément a est dans un ensemble A, nous utilisons le symbole ![]() pour le montrer.
pour le montrer.
Et si quelque chose n’est pas dans un set use ![]() .
.
Exemple: l’ensemble A vaut {1,2,3}. Nous pouvons voir que 1 ![]() A, mais 5
A, mais 5 ![]() A
A
Égalité
Deux ensembles sont égaux s’ils ont précisément le Les mêmes membres. Maintenant, à première vue, ils peuvent ne pas sembler égaux, nous devrons donc peut-être les examiner de près!
Exemple: A et B sont-ils égaux où:
- A est l’ensemble dont les membres sont les quatre premiers nombres entiers positifs
- B = {4, 2, 1, 3}
Vérifions. Ils contiennent tous les deux 1. Ils contiennent tous les deux 2. Et 3, Et 4. Et nous avons vérifié chaque élément des deux ensembles, donc: Oui, ils sont égaux!
Et le signe égal ( =) est utilisé pour montrer l’égalité, nous écrivons donc:
A = B

Sous-ensembles
Lorsque nous définissons un ensemble, si nous prenons des morceaux de cet ensemble, nous pouvons former ce qu’on appelle un sous-ensemble.
En général:
A est un sous-ensemble de B si et seulement si chaque élément de A est dans B.
Utilisons donc cette définition dans quelques exemples.
Essayons un exemple plus difficile.
Sous-ensembles appropriés
Si nous regardons la définition des sous-ensembles et laissons notre esprit vagabonder un peu, nous arrivons à un étrange conclusion.
Soit A un ensemble. Est-ce que chaque élément de A est dans A?
Eh bien, euh, oui bien sûr, non?
Cela signifie donc que A est un sous-ensemble de A. C’est un sous-ensemble de lui-même!
Ceci ne semble pas très approprié, n’est-ce pas? Si nous voulons que nos sous-ensembles soient corrects, nous introduisons (quoi d’autre que) des sous-ensembles appropriés:
A est un sous-ensemble propre de B si et seulement si chaque élément de A est aussi dans B, et il existe au moins un élément dans B qui n’est pas dans A.
Ce petit morceau à la fin est là pour s’assurer que A n’est pas un sous-ensemble propre de lui-même: nous disons que B doit avoir au moins un élément supplémentaire.
Exemple:
{1, 2, 3} est un sous-ensemble de {1, 2, 3}, mais n’est pas un sous-ensemble approprié de {1, 2, 3}.
Exemple:
{1, 2, 3} est un sous-ensemble propre de {1, 2, 3, 4} car l’élément 4 n’est pas dans le premier ensemble.
Remarquez que lorsque A est un sous-ensemble propre de B, il l’est aussi un sous-ensemble de B.
Encore plus de notation
Quand on dit que A est un sous-ensemble de B, on écrit A ![]() B.
B.
Ou nous peut dire que A n’est pas un sous-ensemble de B par A ![]() B (« A n’est pas un sous-ensemble de B »)
B (« A n’est pas un sous-ensemble de B »)
Quand nous parlons de sous-ensembles appropriés, on retire la ligne en dessous et elle devient ainsi A ![]() B ou si l’on veut dire le contraire, A
B ou si l’on veut dire le contraire, A ![]() B.
B.
Ensemble vide (ou nul)
C’est probablement la chose la plus étrange à propos des ensembles.

Par exemple, pensez au jeu de touches de piano sur une guitare.
« Mais attendez! » vous dites: « Il n’y a pas de touches de piano sur un guitare! «
Et vous avez raison. C’est un ensemble sans éléments.
Ceci est connu sous le nom d’Ensemble vide (ou ensemble nul). Il n’y a aucun élément dedans. Pas un. Zéro.
Il est représenté par ![]()
Ou par {} (un ensemble sans éléments)
D’autres exemples de l’ensemble vide sont l’ensemble des pays au sud du pôle sud.
Alors, qu’est-ce qui est si bizarre dans l’ensemble vide? Eh bien, cette partie vient ensuite.
Ensemble vide et sous-ensembles
Revenons donc à notre définition des sous-ensembles. Nous avons un ensemble A. Nous ne le définirons pas. plus que cela, il pourrait s’agir de n’importe quel ensemble. L’ensemble vide est-il un sous-ensemble de A?
Pour en revenir à notre définition des sous-ensembles, si chaque élément de l’ensemble vide est également dans A, alors l’ensemble vide est un sous-ensemble de A. Mais que faire si nous n’ont aucun élément?
Il faut une introduction à la logique pour comprendre cela, mais cette affirmation est celle qui est « vide » ou « trivialement » vraie.
Une bonne façon de penser c’est: nous ne pouvons trouver aucun élément de l’ensemble vide qui ne soit pas dans A, il faut donc que tous les éléments de l’ensemble vide soient dans A.
Donc la réponse à la question posée est un oui retentissant.
L’ensemble vide est un sous-ensemble de chaque ensemble, y compris l’ensemble vide lui-même.
Ordre
Non, pas l’ordre des éléments. Dans les ensembles, l’ordre dans lequel se trouvent les éléments n’a pas d’importance.
Exemple: {1,2,3,4} est le même ensemble que {3,1,4,2}
Quand nous disons ordre en ensembles, nous entendons la taille de l’ensemble.
Un autre (meilleur) nom pour cela est la cardinalité.
Un ensemble fini a un ordre fini (ou cardinalité). Un ensemble infini a un ordre (ou cardinalité) infini.
Pour les ensembles finis, l’ordre (ou cardinalité) est le nombre d’éléments.
Exemple: {10, 20, 30, 40} a un ordre de 4.
Pour les ensembles infinis, tout ce que nous pouvons dire, c’est que l’ordre est infini. Curieusement, nous pouvons dire avec les ensembles que certains infinis sont plus grands que d’autres, mais c’est un sujet plus avancé dans les ensembles.
Arg! Pas plus de notation!
Non, je plaisante. Plus de notation.
par
et