Tanulási célok
- Adja meg a de Broglie hullámegyenletet.
- Használja ez az egyenlet egy mozgó objektum hullámhosszának kiszámításához.
Bohr modelljén túl
Bohr atommodellje értékes volt annak bemutatásában, hogy az elektronok hogyan képesek voltak az energia elnyelésére és felszabadítására, valamint az atomemissziós spektrumok létrehozásának módjára. A modell azonban nem igazán magyarázta meg, miért kellene az elektronoknak csak rögzített körpályákon létezniük, ahelyett, hogy korlátlan számú, különböző energiájú pályán léteznének. Annak érdekében, hogy megmagyarázzák, miért kvantálják az atomenergia-állapotokat, a tudósoknak át kellett gondolniuk azt a módot, ahogyan szemlélik az elektron természetét és mozgását.
Planck forró tárgyak emissziós spektrumának vizsgálata és a fotoelektromos hatással kapcsolatos későbbi vizsgálatok bebizonyították, hogy a fény képes hullámként és részecskeként is viselkedni. Ésszerűnek tűnt azon tűnődni, hogy az elektronoknak is lehet-e kettős hullám-részecske jellege. 1924-ben Louis de Broglie (1892–1987) francia tudós levezetett egy egyenletet, amely leírta bármely részecske hullámtermészetét. Különösen bármely mozgó objektum hullámhosszát (λ) adja meg:
\ displaystyle \ lambda = \ frac {h} {mv}
Ebben az egyenletben h Planck állandója , m a részecske tömege kg-ban, és v a részecske sebessége m / s-ban. Az alábbi probléma megmutatja, hogyan lehet kiszámítani az elektron hullámhosszát.
Ha egy 0,145 kg-os 40 m / s sebességgel dobott baseball hullámhosszát számolnánk, akkor egy rendkívül rövid hullámhossz nagyságrendileg 10−34 m. Ezt a hullámhosszat még fejlett tudományos berendezésekkel sem lehet kimutatni. Valójában, miközben minden tárgy hullámmozgással mozog, soha nem vesszük észre, mert a hullámhosszak túl rövidek. Másrészt a mérhető hullámhosszú részecskék mind nagyon kicsiek. Az elektron hullám jellege azonban kulcsfontosságú fejleménynek bizonyult az elektron természetének új megértésében. Az atom magja körül egy adott térbe szorított elektron csak úgy mozoghat az atom körül, hogy elektronhulláma helyesen “illeszkedjen” az atom méretéhez. Ez azt jelenti, hogy az elektronhullámok frekvenciái kvantáltak. Az E = hv egyenlet alapján a kvantált frekvenciák azt jelentik, hogy az elektronok csak bizonyos energiákon létezhetnek egy atomban, amint azt Bohr korábban elméletileg megfogalmazta.
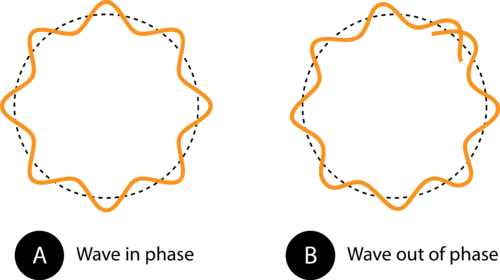
1. ábra: A pálya kerülete (A) -ben lehetővé teszi az elektronhullám tökéletes illeszkedését a pályára. Ez egy megengedett pálya. A (B) -ben az elektronhullám nem megfelelően illeszkedik a pályára, ezért ez a pálya nem megengedett.
Összefoglalás
- A deBroglie hullámegyenletek lehetővé teszik minden mozgó hullámhosszának kiszámítását. objektum.
- Ahogy az elektron sebessége csökken, hullámhossza nő.
Gyakorlat
Használja a linket alatt gyakorolhatja a számításokat a deBroglie hullámegyenlet:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Áttekintés
- Mi nem magyarázta a Bohr-modell?
- Állítsa le a deBroglie-hullámegyenletet.
- Mi történik, ha az elektron sebessége csökken?