Beispiel: Zufallszahlen
Angenommen, wir betrachten reelle Zahlen, die zufällig zwischen 0 und 1 ausgewählt wurden und für die wir \ aufzeichnen (X_1 \), die auf eine Dezimalstelle abgeschnittene Zufallszahl. Beispielsweise wird die Zahl 0.07491234008 als 0.0 aufgezeichnet (da die erste Dezimalstelle Null ist). Beachten Sie, dass dies bedeutet, dass wir nicht runden, sondern abschneiden. Wenn der Mechanismus, der diese Zahlen erzeugt, keine Position im Intervall \ ((0,1) \) bevorzugt, ist die Verteilung der Zahlen, die wir erhalten, so, dass
\
dies ein diskreter Zufall ist variabel, mit der gleichen Wahrscheinlichkeit für jedes der zehn möglichen Ergebnisse.
\
Die Verteilungen von \ (X_1 \) und \ (X_2 \) sind in Abbildung 2 dargestellt.
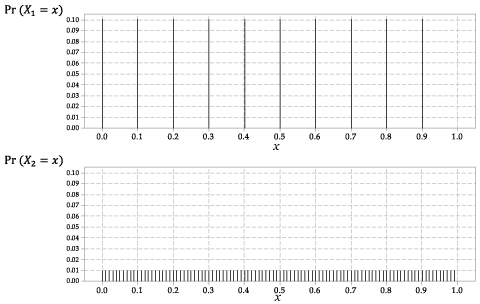
Detaillierte Beschreibung
Abbildung 2: Die Wahrscheinlichkeitsfunktionen \ (p_ {X_1} (x) \) für \ (X_1 \) und \ (p_ {X_2} (x) \) für \ (X_2 \).
Excel verfügt über eine Funktion, die reelle Zahlen zwischen 0 und 1 erzeugt und so gewählt wird, dass keine Position im Intervall bevorzugt wird \ ( (0,1) \). Wenn Sie \ (\ sf \ text {= RAND ()} \) in eine Zelle eingeben und die Eingabetaste drücken, erhalten Sie eine solche Nummer. Erhöhen Sie die Anzahl der in der Zelle angezeigten Dezimalstellen. Fahren Sie fort, bis Sie am Ende der Zahl viele Nullen erhalten. Möglicherweise müssen Sie die Größe der Zelle erhöhen. Ihre Tabelle sollte wie in Abbildung 3 aussehen, obwohl die spezifische Zahl natürlich anders sein wird… sie ist schließlich zufällig!
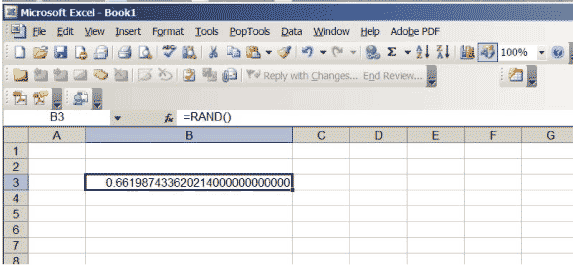
Abbildung 3: Eine Excel-Tabelle mit einer Zufallszahl zwischen 0 und 1.
Wenn Sie an dieser Stelle wiederholt die Taste „F9“ drücken, wird eine Folge von Zufallszahlen zwischen 0 und 1 angezeigt 1. Aus diesen Untersuchungen geht hervor, dass Excel tatsächlich Beobachtungen für die Zufallsvariable \ (X_ {15} \) erzeugt, die ersten 15 Dezimalstellen der Zahl. Die Wahrscheinlichkeit, dass eine bestimmte dieser Zahlen auftritt, ist also \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0,4) & = \ Pr (X_1 = 0,3) = 0,1, \\\\ \ Pr (0,3 \ leq X_2 < 0,4) & = \ Pr (X_2 = 0,30) + \ Pr (X_2 = 0,31) + \ dots + \ Pr (X_2 = 0,39) \\\\ & = 10 \ mal 0,01 = 0,1, \\\\ \ Pr (0,3 \ leq X_3 < 0,4) & = 10 ^ 2 \ mal 10 ^ {- 3} = 0,1, \\\\ \ Pr (0,3 \ leq X_4 < 0,4) & = 10 ^ 3 \ times 10 ^ {- 4} = 0.1, \\\\ & \ vdots \\\\ \ Pr (0.3 \ leq X_k < 0,4) & = 10 ^ {k-1} \ times 10 ^ {- k} = 0,1, \\\\ & \ vdots \ end {align *}
Wenn wir die Verteilung mit immer mehr möglichen diskreten Werten immer feiner machen, liegt die Wahrscheinlichkeit, dass eine dieser diskreten Zufallsvariablen im Intervall liegt \ (
Zum Beispiel \ (\ Pr (0,3 \ leq U \ leq 0,4) = 0,4 – 0,3 = 0,1 \).
Das cdf dieser Zufallsvariablen \ (F_U (u) \) ist daher sehr einfach. Es ist
\
Die folgende Abbildung zeigt den Graphen der kumulativen Verteilungsfunktion von \ (U \).
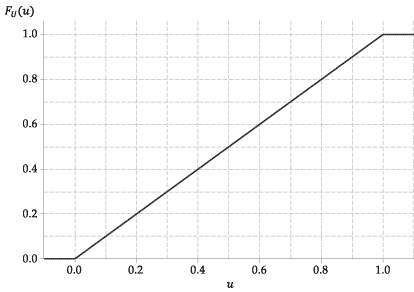
Abbildung 4: Die kumulative Verteilungsfunktion von \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Möglicherweise haben Sie stellten einen Unterschied in der Behandlung des Intervalls zwischen 0,3 und 0,4 im kontinuierlichen Fall im Vergleich zu den diskreten Fällen fest. In allen diskreten Fällen wurden die Obergrenzen \ (0,4, 0,40, 0,400, \ Punkte \) ausgeschlossen, während sie für die kontinuierliche Zufallsvariable enthalten sind. Wann immer es sich um diskrete Zufallsvariablen handelt, spielt es oft eine Rolle, ob die Ungleichung streng ist oder nicht, und es ist Vorsicht geboten. Zum Beispiel
\ \