Obiettivi di apprendimento
- Indica l’equazione d’onda di de Broglie.
- Usa questa equazione per calcolare la lunghezza d’onda di un oggetto in movimento.
Oltre il modello di Bohr
Il modello dell’atomo di Bohr era prezioso per dimostrare come gli elettroni erano in grado di assorbire e rilasciare energia e come venivano creati gli spettri di emissione atomica. Tuttavia, il modello non spiegava realmente perché gli elettroni dovessero esistere solo in orbite circolari fisse piuttosto che poter esistere in un numero illimitato di orbite tutte con energie diverse. Per spiegare perché gli stati di energia atomica sono quantizzati, gli scienziati dovevano ripensare al modo in cui hanno visto la natura dell’elettrone e il suo movimento.
Indagine di Planck sugli spettri di emissione di oggetti caldi e gli studi successivi sull’effetto fotoelettrico avevano dimostrato che la luce era in grado di comportarsi sia come un’onda che come una particella. Sembrava ragionevole chiedersi se gli elettroni potessero anche avere una doppia natura di particelle d’onda. Nel 1924, lo scienziato francese Louis de Broglie (1892-1987) derivò un’equazione che descriveva la natura ondulatoria di ogni particella. In particolare, la lunghezza d’onda (λ) di qualsiasi oggetto in movimento è data da:
\ displaystyle \ lambda = \ frac {h} {mv}
In questa equazione, h è la costante di Planck , m è la massa della particella in kg e v è la velocità della particella in m / s. Il problema seguente mostra come calcolare la lunghezza d’onda dell’elettrone.
Se dovessimo calcolare la lunghezza d’onda di una palla da baseball di 0,145 kg lanciata a una velocità di 40 m / s, otterremmo una lunghezza d’onda estremamente corta lunghezza d’onda dell’ordine di 10-34 m. Questa lunghezza d’onda è impossibile da rilevare anche con apparecchiature scientifiche avanzate. Infatti, mentre tutti gli oggetti si muovono con un movimento ondulatorio, non lo notiamo mai perché le lunghezze d’onda sono troppo brevi. D’altra parte, le particelle con lunghezze d’onda misurabili sono tutte molto piccole. Tuttavia, la natura ondulatoria dell’elettrone si è rivelata uno sviluppo chiave in una nuova comprensione della natura dell’elettrone. Un elettrone che è confinato in uno spazio particolare attorno al nucleo di un atomo può solo muoversi intorno a quell’atomo in modo tale che la sua onda elettronica “si adatti” correttamente alla dimensione dell’atomo, il che significa che le frequenze delle onde elettroniche sono quantizzate. Sulla base dell’equazione E = hv, le frequenze quantizzate significano che gli elettroni possono esistere solo in un atomo a energie specifiche, come Bohr aveva precedentemente teorizzato.
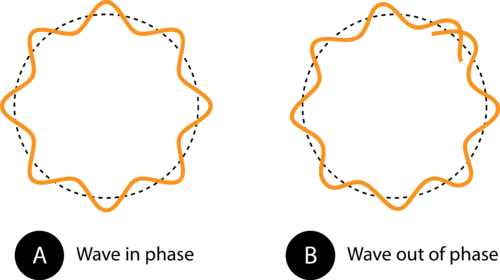
Figura 1. La circonferenza dell’orbita in (A) consente all’onda dell’elettrone di adattarsi perfettamente all’orbita. Questa è un’orbita consentita. In (B), l’onda dell’elettrone no adattarsi correttamente all’orbita, quindi questa orbita non è consentita.
Riepilogo
- Le equazioni d’onda di deBroglie consentono il calcolo della lunghezza d’onda di qualsiasi movimento oggetto.
- Man mano che la velocità dell’elettrone diminuisce, la sua lunghezza d’onda aumenta.
Pratica
Usa il link di seguito per fare pratica con i calcoli usando l’equazione dell’onda deBroglie:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Rivedi
- Cosa il modello di Bohr non spiega?
- Indica l’equazione delle onde di deBroglie.
- Cosa succede quando la velocità dell’elettrone diminuisce?