例:乱数
0から1の間でランダムに選択された実数を考慮して\を記録するとします。 (X_1 \)、小数点以下1桁に切り捨てられた乱数。たとえば、数値0.07491234008は0.0として記録されます(小数点以下第1位がゼロであるため)。これは、丸めではなく切り捨てを意味することに注意してください。これらの数値を生成するメカニズムが区間\((0,1)\)内のどの位置にも優先しない場合、取得される数値の分布は次のようになります。
\
これは離散確率変数です。変数、10の可能な結果のそれぞれについて同じ確率で。
\
\(X_1 \)と\(X_2 \)の分布を図2に示します。
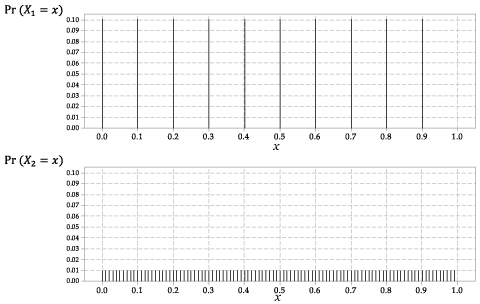
詳細な説明
図2:\(X_1 \)と\(p_の確率関数\(p_ {X_1}(x)\) {X_2}(x)\)for \(X_2 \)。
Excelには、0から1までの実数を生成する関数があり、区間\(のどの位置も優先されないように選択されています。 (0,1)\)。セルに\(\ sf \ text {= RAND()} \)と入力してリターンキーを押すと、そのような数値が得られます。セルに表示される小数点以下の桁数を増やします。数字の最後にたくさんのゼロが表示されるまで続けます。セルのサイズを大きくする必要がある場合があります。スプレッドシートは図3のようになりますが、もちろん特定の数は異なります…結局のところランダムです!
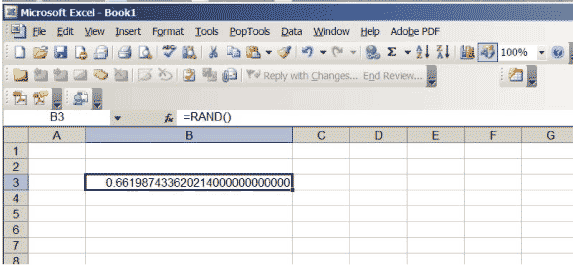
図3:0から1までの乱数を含むExcelスプレッドシート。
この時点でキー「F9」を繰り返し押すと、すべて0から1までの一連の乱数が表示されます。 1.これらを調べると、Excelは実際に乱数の最初の15桁である乱数\(X_ {15} \)の観測値を生成しているように見えます。したがって、これらの数値の特定の1つが発生する可能性は\(10 ^ {-15} \)です。
\ begin {align *} \ Pr(0.3 \ leq X_1 < 0.4)& = \ Pr(X_1 = 0.3)= 0.1、\\\\ \ Pr(0.3 \ leq X_2 < 0.4)& = \ Pr(X_2 = 0.30)+ \ Pr(X_2 = 0.31)+ \ dots + \ Pr(X_2 = 0.39)\\\\ & = 10 \ times 0.01 = 0.1、\\\\ \ Pr(0.3 \ leq X_3 < 0.4)& = 10 ^ 2 \ times 10 ^ {-3} = 0.1、\\\\ \ Pr(0.3 \ leq X_4 < 0.4)& = 10 ^ 3 \ times 10 ^ {-4} = 0.1、\\\\ & \ vdots \\\\ \ Pr(0.3 \ leq X_k < 0.4)& = 10 ^ {k-1} \ times 10 ^ {-k} = 0.1、\\\\ & \ vdots \ end {align *}
可能な離散値が増えるにつれて、分布がますます細かくなり、これらの離散確率変数のいずれかが区間内にある確率\(
たとえば、\(\ Pr(0.3 \ leq U \ leq 0.4)= 0.4-0.3 = 0.1 \)。
この確率変数の累積分布関数\(F_U(u) \)、したがって、非常に単純です。
\
次の図は、\(U \)の累積分布関数のグラフを示しています。
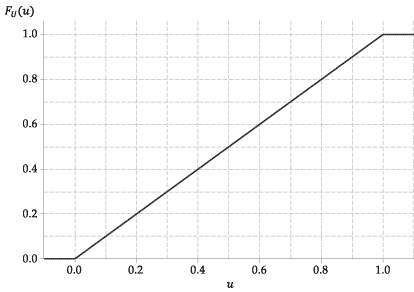
図4:\(U \ stackrel {\ mathrm {d}} {=} \ mathrm {U}(0,1)\)の累積分布関数。
離散の場合と比較して、連続の場合の0.3と0.4の間の間隔の処理方法に違いがあることに気づきました。すべての離散ケースで、上限\(0.4、0.40、0.400、\ dots \)が除外され、連続確率変数の場合は含まれています。離散確率変数を扱うときはいつでも、不等式が厳密であるかどうかが重要であることが多く、注意が必要です。たとえば、
\ \