예 : 난수
0과 1 사이에서 무작위로 선택된 실수를 고려한다고 가정합니다. (X_1 \), 소수점 한 자리로 잘린 난수. 예를 들어 숫자 0.07491234008은 0.0으로 기록됩니다 (소수점 첫 번째 자리가 0이므로). 이것은 우리가 반올림이 아니라 잘림을 의미합니다. 이 숫자를 생성하는 메커니즘이 \ ((0,1) \) 구간의 위치에 대해 선호하지 않는 경우, 우리가 얻는 숫자의 분포는 다음과 같을 것입니다.
\
이것은 이산 난수입니다 10 가지 가능한 결과 각각에 대해 동일한 확률로 변수.
\
\ (X_1 \) 및 \ (X_2 \)의 분포는 그림 2에 나와 있습니다.
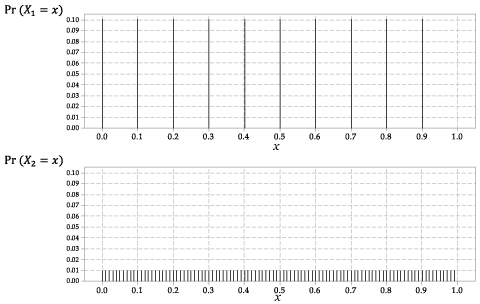
자세한 설명
그림 2 : \ (X_1 \) 및 \ (p_에 대한 확률 함수 \ (p_ {X_1} (x) \) {X_2} (x) \) for \ (X_2 \).
Excel에는 0과 1 사이의 실수를 생성하는 함수가 있으며, \ (간격의 위치에 대한 선호도가 없도록 선택되었습니다. (0,1) \). 셀에 \ (\ sf \ text {= RAND ()} \)를 입력하고 Return 키를 누르면 해당 숫자를 얻을 수 있습니다. 셀에 표시된 소수 자릿수를 늘립니다. 숫자 끝에 0이 많이 나올 때까지 계속 진행하십시오. 셀 크기를 늘려야 할 수도 있습니다. 물론 특정 숫자는 다를 수 있지만 스프레드 시트는 그림 3과 같아야합니다. 결국 무작위입니다!
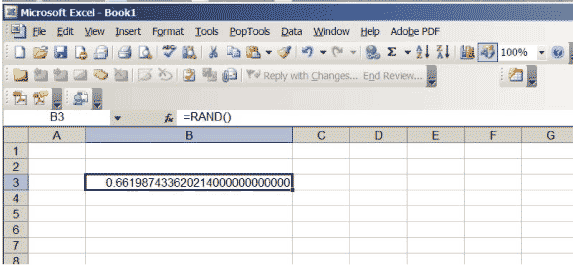
그림 3 : 0과 1 사이의 임의의 숫자가있는 Excel 스프레드 시트
이 시점에서 “F9″키를 반복적으로 누르면 0과 1 사이의 일련의 임의 숫자가 표시됩니다. 1.이를 조사한 결과 Excel은 숫자의 처음 15 자리 인 랜덤 변수 \ (X_ {15} \)에 대한 관측치를 실제로 생성하는 것으로 보입니다. 따라서 이러한 숫자 중 특정 숫자가 발생할 확률은 \ (10 ^ {-15} \)입니다.
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ \ Pr (0.3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0.30) + \ Pr (X_2 = 0.31) + \ dots + \ Pr (X_2 = 0.39) \\\\ & = 10 \ times 0.01 = 0.1, \\\\ \ Pr (0.3 \ leq X_3 < 0.4) & = 10 ^ 2 \ times 10 ^ {-3} = 0.1, \\\\ \ Pr (0.3 \ leq X_4 < 0.4) & = 10 ^ 3 \ times 10 ^ {-4} = 0.1, \\\\ & \ vdots \\\\ \ Pr (0.3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ times 10 ^ {-k} = 0.1, \\\\ & \ vdots \ end {align *}
더 많은 가능한 이산 값을 사용하여 분포를 더 미세하고 미세하게 만들면 이러한 이산 랜덤 변수가 구간에있을 확률 \ (
예 : \ (\ Pr (0.3 \ leq U \ leq 0.4) = 0.4-0.3 = 0.1 \)
이 랜덤 변수의 cdf, \ (F_U (u) \), 따라서 매우 간단합니다. 이것은
\
다음 그림은 \ (U \)의 누적 분포 함수 그래프입니다.
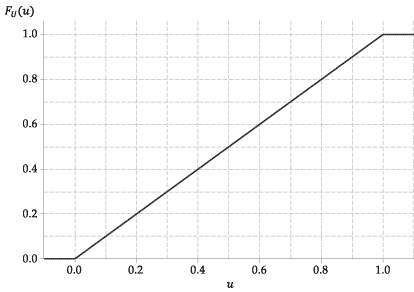
그림 4 : \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \)의 누적 분포 함수
이산 사례와 비교하여 연속 사례에서 0.3과 0.4 사이의 간격이 처리되는 방식의 차이를 발견했습니다. 모든 불연속 경우에서 상한 \ (0.4, 0.40, 0.400, \ dots \)는 제외되고 연속 랜덤 변수의 경우 포함됩니다. 이산 확률 변수를 다룰 때마다 불평등이 엄격한 지 자주 중요하지 않으며주의가 필요합니다. 예 :
\ \