Eksempel: Tilfeldige tall
Anta at vi betrakter reelle tall tilfeldig valgt mellom 0 og 1, som vi registrerer \ (X_1 \), det tilfeldige tallet avkortet til en desimal. For eksempel er tallet 0,07491234008 registrert som 0,0 (som første desimal er null). Merk at dette betyr at vi ikke avrunder, men avkorter. Hvis mekanismen som genererer disse tallene ikke foretrekker noen posisjon i intervallet \ ((0,1) \), vil fordelingen av tallene vi får være slik at
\
Dette er en diskret tilfeldig variabel, med samme sannsynlighet for hvert av de ti mulige resultatene.
\
Fordelingen av \ (X_1 \) og \ (X_2 \) er vist i figur 2.
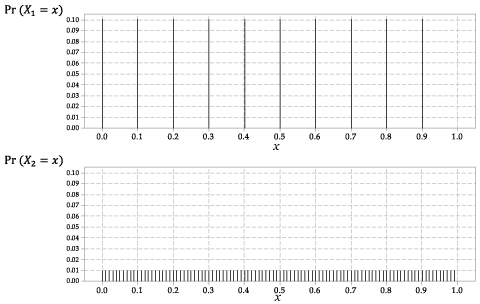
Detaljert beskrivelse
Figur 2: Sannsynlighetsfunksjonene \ (p_ {X_1} (x) \) for \ (X_1 \) og \ (p_ {X_2} (x) \) for \ (X_2 \).
Excel har en funksjon som produserer reelle tall mellom 0 og 1, valgt slik at det ikke foretrekkes noen posisjon i intervallet \ ( (0,1) \). Hvis du skriver inn \ (\ sf \ text {= RAND ()} \) i en celle og trykker på retur, får du et slikt tall. Øk antall desimaler som vises i cellen. Fortsett til du får mange nuller på slutten av nummeret; du må kanskje øke størrelsen på cellen. Regnearket ditt skal se ut som figur 3, selv om det spesifikke nummeret selvfølgelig vil være annerledes … det er tross alt tilfeldig!
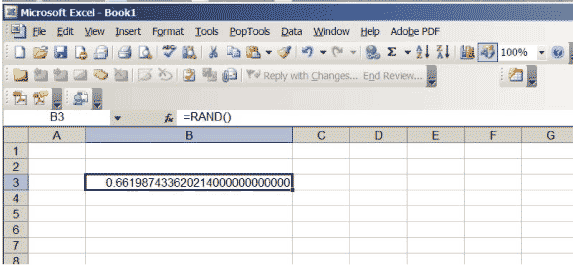
Figur 3: Et Excel-regneark med et tilfeldig tall mellom 0 og 1.
Hvis du trykker på tasten «F9» gjentatte ganger på dette tidspunktet, vil du se en sekvens av tilfeldige tall, alt mellom 0 og 1. Fra å undersøke disse ser det ut til at Excel faktisk produserer observasjoner på den tilfeldige variabelen \ (X_ {15} \), de første 15 desimalene i tallet. Så sjansen for at et spesifikt av disse tallene oppstår er \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ \ Pr (0.3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0.30) + \ Pr (X_2 = 0.31) + \ prikker + \ Pr (X_2 = 0.39) \\\\ & = 10 \ ganger 0.01 = 0.1, \\\\ \ Pr (0.3 \ leq X_3 < 0.4) & = 10 ^ 2 \ ganger 10 ^ {- 3} = 0.1, \\\\ \ Pr (0.3 \ leq X_4 < 0.4) & = 10 ^ 3 \ ganger 10 ^ {- 4} = 0.1, \\\\ & \ vdots \\\\ \ Pr (0,3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ ganger 10 ^ {- k} = 0.1, \\\\ & \ vdots \ end {align *}
Når vi gjør fordelingen finere og finere, med flere og flere mulige diskrete verdier, ligger sannsynligheten for at noen av disse diskrete tilfeldige variablene ligger i intervallet \ (
For eksempel \ (\ Pr (0.3 \ leq U \ leq 0.4) = 0.4 – 0.3 = 0.1 \).
Cdf for denne tilfeldige variabelen, \ (F_U (u) \), er derfor veldig enkelt. Det er
\
Figuren nedenfor viser grafen for den kumulative fordelingsfunksjonen til \ (U \).
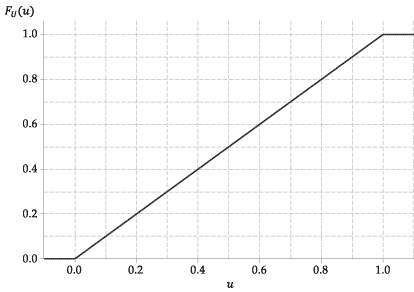
Figur 4: Den kumulative fordelingsfunksjonen til \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Du kan ha la merke til en forskjell i hvordan intervallet mellom 0,3 og 0,4 ble behandlet i det kontinuerlige tilfellet, sammenlignet med de diskrete tilfellene. I alle de diskrete tilfellene ble de øvre grensene \ (0.4, 0.40, 0.400, \ dots \) ekskludert, mens den for den kontinuerlige tilfeldige variabelen er inkludert. Hver gang vi har å gjøre med diskrete tilfeldige variabler, er det ofte viktig med ulikhet eller ikke, og det er nødvendig med forsiktighet. For eksempel
\ \