Leerdoelen
- Geef de golfvergelijking van de Broglie.
- Gebruik deze vergelijking om de golflengte van een bewegend object te berekenen.
Beyond Bohr’s Model
Bohr’s model van het atoom was waardevol om te laten zien hoe elektronen waren in staat om energie te absorberen en af te geven en hoe atomaire emissiespectra werden gecreëerd. Het model legde echter niet echt uit waarom elektronen alleen in vaste cirkelvormige banen zouden moeten bestaan in plaats van te kunnen bestaan in een onbeperkt aantal banen met allemaal verschillende energieën. Om uit te leggen waarom atoomenergietoestanden worden gekwantiseerd, moesten wetenschappers de manier waarop ze de aard van het elektron en zijn beweging zagen, heroverwegen.
Planck’s onderzoek naar de emissiespectra van hete objecten en de daaropvolgende studies naar het foto-elektrische effect hadden aangetoond dat licht zich zowel als golf als als deeltje kan gedragen. Het leek redelijk om me af te vragen of elektronen ook een tweevoudig golfdeeltje zouden kunnen hebben. In 1924 leidde de Franse wetenschapper Louis de Broglie (1892–1987) een vergelijking af die de golfkarakteristiek van elk deeltje beschreef. In het bijzonder wordt de golflengte (λ) van elk bewegend object gegeven door:
\ displaystyle \ lambda = \ frac {h} {mv}
In deze vergelijking is h de constante van Planck , m is de massa van het deeltje in kg, en v is de snelheid van het deeltje in m / s. Het onderstaande probleem laat zien hoe we de golflengte van het elektron kunnen berekenen.
Als we de golflengte zouden berekenen van een honkbal van 0,145 kg gegooid met een snelheid van 40 m / s, zouden we een extreem korte golflengte in de orde van 10−34 m. Deze golflengte is zelfs met geavanceerde wetenschappelijke apparatuur onmogelijk te detecteren. Inderdaad, terwijl alle objecten met golfachtige beweging bewegen, merken we het nooit op omdat de golflengten veel te kort zijn. Aan de andere kant zijn deeltjes met meetbare golflengten allemaal erg klein. De golfkarakteristiek van het elektron bleek echter een belangrijke ontwikkeling te zijn in een nieuw begrip van de aard van het elektron. Een elektron dat zich beperkt tot een bepaalde ruimte rond de atoomkern kan alleen zo rond dat atoom bewegen dat zijn elektronengolf correct ‘past’ bij de grootte van het atoom, wat betekent dat de frequenties van elektronengolven worden gekwantiseerd. Gebaseerd op de E = hv-vergelijking, betekenen de gekwantiseerde frequenties dat elektronen alleen in een atoom kunnen bestaan bij specifieke energieën, zoals Bohr eerder had getheoretiseerd.
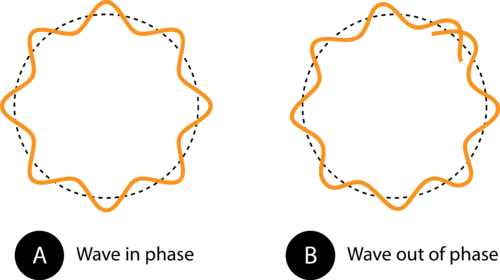
Figuur 1. Door de omtrek van de baan in (A) past de elektronengolf perfect in de baan. Dit is een toegestane baan. In (B) doet de elektronengolf niet passen goed in de baan, dus deze baan is niet toegestaan.
Samenvatting
- Met de deBroglie-golfvergelijkingen kan de golflengte van elke bewegende object.
- Naarmate de snelheid van het elektron afneemt, neemt zijn golflengte toe.
Oefenen
Gebruik de link hieronder om berekeningen te oefenen met de deBroglie-golfvergelijking:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Review
- Wat heeft het Bohr-model dit niet uitgelegd?
- Geef de deBroglie-golfvergelijking.
- Wat gebeurt er als de snelheid van het elektron afneemt?