Przykład: liczby losowe
Załóżmy, że rozważamy liczby rzeczywiste losowo wybrane z zakresu od 0 do 1, dla których zapisujemy \ (X_1 \), liczba losowa obcięta do jednego miejsca po przecinku. Na przykład liczba 0,07491234008 jest zapisywana jako 0,0 (pierwsze miejsce po przecinku to zero). Zwróć uwagę, że oznacza to, że nie zaokrąglamy, ale skracamy. Jeśli mechanizm generujący te liczby nie ma preferencji dla żadnej pozycji w przedziale \ ((0,1) \), to rozkład otrzymanych liczb będzie taki, że
\
Jest to dyskretna losowa zmienna, z takim samym prawdopodobieństwem dla każdego z dziesięciu możliwych wyników.
\
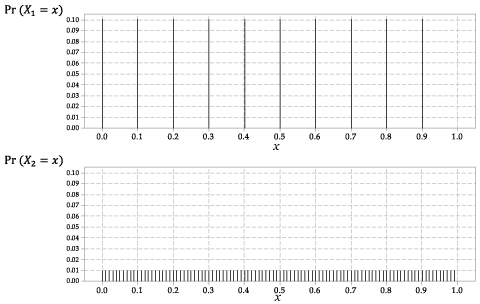
Rozkłady \ (X_1 \) i \ (X_2 \) pokazano na rysunku 2.
Szczegółowy opis
Rysunek 2: Funkcje prawdopodobieństwa \ (p_ {X_1} (x) \) dla \ (X_1 \) i \ (p_ {X_2} (x) \) dla \ (X_2 \).
Excel ma funkcję, która generuje liczby rzeczywiste od 0 do 1, wybrane tak, aby nie było preferencji dla żadnej pozycji w interwale \ ( (0,1) \). Jeśli wpiszesz \ (\ sf \ text {= RAND ()} \) w komórce i naciśniesz return, uzyskasz taką liczbę. Zwiększ liczbę miejsc dziesiętnych wyświetlanych w komórce. Kontynuuj, aż uzyskasz dużo zer na końcu liczby; może być konieczne zwiększenie rozmiaru komórki. Twój arkusz kalkulacyjny powinien wyglądać jak na rysunku 3, chociaż oczywiście konkretna liczba będzie inna… w końcu jest losowa!
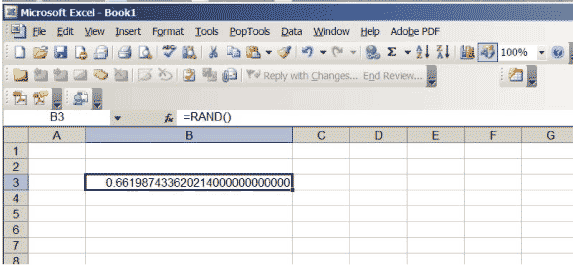
Rysunek 3: Arkusz kalkulacyjny Excel z losową liczbą z zakresu od 0 do 1.
Jeśli w tym miejscu kilkakrotnie naciśniesz klawisz „F9”, zobaczysz sekwencję liczb losowych, wszystkie od 0 do 1. Z ich analizy wynika, że program Excel w rzeczywistości tworzy obserwacje zmiennej losowej \ (X_ {15} \), pierwszych 15 miejsc dziesiętnych liczby. Zatem prawdopodobieństwo wystąpienia którejkolwiek z tych liczb wynosi \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0,3 \ leq X_1 < 0,4) & = \ Pr (X_1 = 0.3) = 0,1, \\\\ \ Pr (0,3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0,30) + \ Pr (X_2 = 0,31) + \ dots + \ Pr (X_2 = 0,39) \\\\ & = 10 \ times 0,01 = 0,1, \\\\ \ Pr (0,3 \ leq X_3 < 0,4) & = 10 ^ 2 \ times 10 ^ {- 3} = 0,1, \\\\ \ Pr (0,3 \ leq X_4 < 0,4) & = 10 ^ 3 \ times 10 ^ {- 4} = 0,1, \\\\ & \ vdots \\\\ \ Pr (0,3 \ leq X_k < 0,4) & = 10 ^ {k-1} \ times 10 ^ {- k} = 0,1, \\\\ & \ vdots \ end {align *}
W miarę jak robimy dokładniejszy i dokładniejszy rozkład, z coraz większą liczbą możliwych wartości dyskretnych, prawdopodobieństwo, że którakolwiek z tych dyskretnych zmiennych losowych znajduje się w przedziale \ (
Na przykład \ (\ Pr (0,3 \ leq U \ leq 0,4) = 0,4 – 0,3 = 0,1 \).
Cdf tej zmiennej losowej, \ (F_U (u) \) jest zatem bardzo prosta. To jest
\
Poniższy rysunek przedstawia wykres funkcji dystrybucji skumulowanej \ (U \).
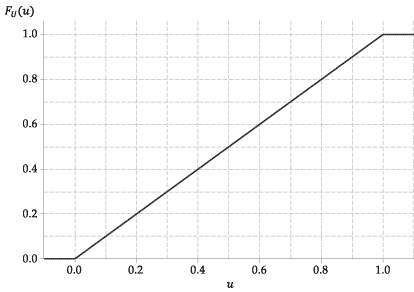
Rysunek 4: Skumulowana funkcja dystrybucji \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Być może zauważyli różnicę w traktowaniu przedziału od 0,3 do 0,4 w przypadku ciągłym w porównaniu z przypadkami dyskretnymi. We wszystkich dyskretnych przypadkach wykluczono górne granice \ (0,4, 0,40, 0,400, \ kropki \), natomiast dla ciągłej zmiennej losowej została ona uwzględniona. Ilekroć mamy do czynienia z dyskretnymi zmiennymi losowymi, często ma znaczenie, czy nierówność jest ścisła, czy nie, i należy zachować ostrożność. Na przykład
\ \