O que é desvio padrão? | STDEV.P | STDEV.S | Variância
Esta página explica como calcular o desvio padrão com base em toda a população usando a função DESVPAD.P no Excel e como estimar o desvio padrão com base em uma amostra usando a função DESVPAD.S no Excel.
O que é desvio padrão?
O desvio padrão é um número que indica a que distância os números estão de sua média.
1. Por exemplo, os números abaixo têm uma média (média) de 10.
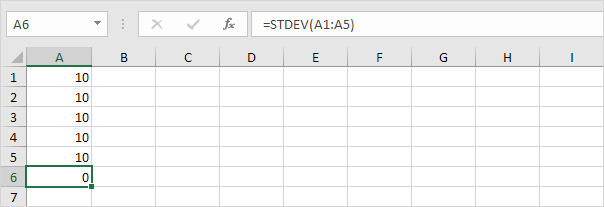
Explicação: os números são todos iguais e significa que não há variação. Como resultado, os números têm um desvio padrão de zero. A função STDEV é uma função antiga. O Microsoft Excel recomenda o uso da nova função STEDV.S, que produz exatamente o mesmo resultado.
2. Os números abaixo também têm uma média (média) de 10.
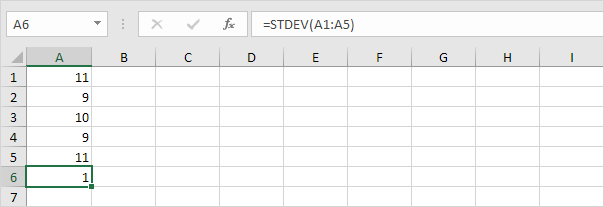
Explicação: os números estão próximos da média. Como resultado, os números têm um baixo desvio padrão.
3. Os números abaixo também têm uma média (média) de 10.
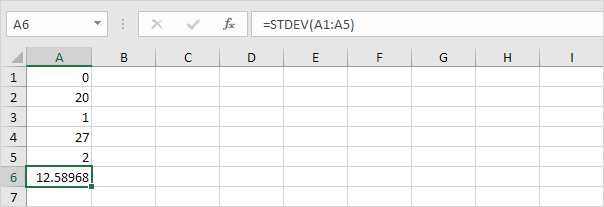
Explicação: os números estão espalhados. Como resultado, os números têm um desvio padrão alto.
STDEV.P
A função STDEV.P (o P significa População) no Excel calcula o desvio padrão com base em toda a população. Por exemplo, você está ensinando um grupo de 5 alunos. Você tem os resultados dos testes de todos os alunos. A população inteira consiste em 5 pontos de dados. A função STDEV.P usa a seguinte fórmula:
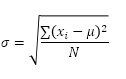
Neste exemplo, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (média), N = 5 (número de pontos de dados).
1. Calcule a média (μ).
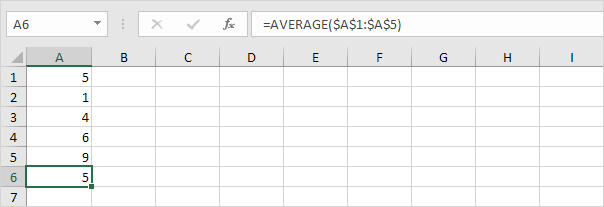
2. Para cada número, calcule a distância até a média.
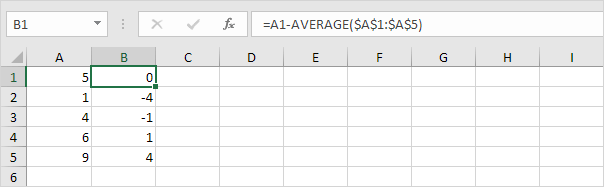
3. Para cada número, eleve ao quadrado esta distância.
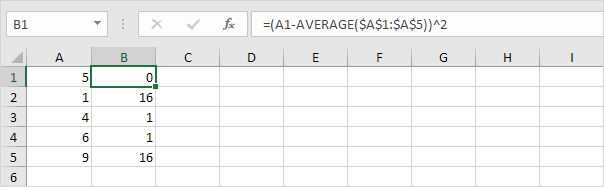
4. Some (∑) esses valores.
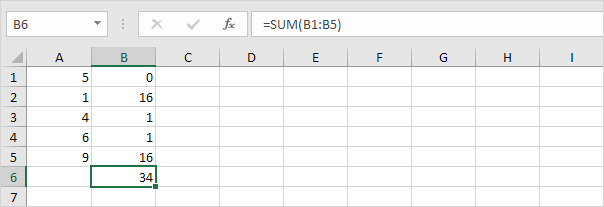
5. Divida pelo número de pontos de dados (N = 5).
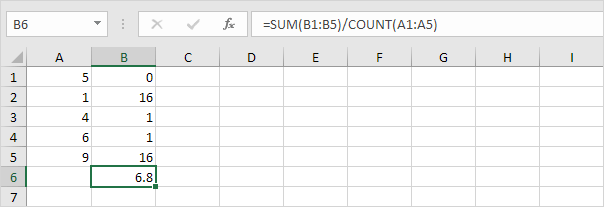
6. Obtenha a raiz quadrada.
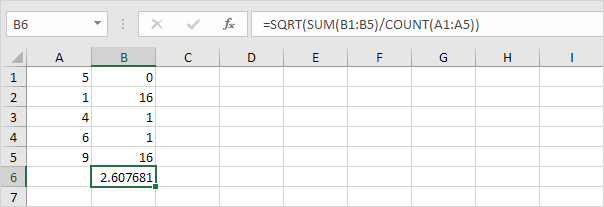
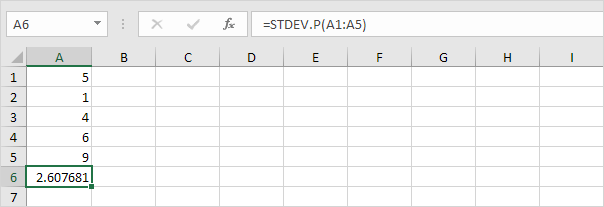
7. Felizmente, a função STDEV.P no Excel pode executar todas essas etapas para você.
STDEV.S
A função STDEV.S (o S significa Amostra) no Excel estima o desvio padrão com base em uma amostra. Por exemplo, você está ensinando um grande grupo de alunos. Você só tem as pontuações de 5 alunos no teste. O tamanho da amostra é igual a 5. A função STDEV.S usa a seguinte fórmula:
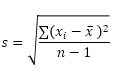
Neste exemplo, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (mesmos números que acima), x̄ = 5 (amostra média), n = 5 (tamanho da amostra).
1. Repita as etapas 1 a 5 acima, mas na etapa 5 divida por n-1 em vez de N.
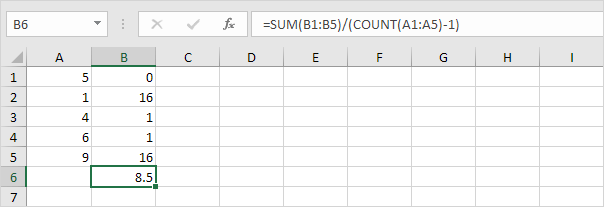
2. Tire a raiz quadrada.
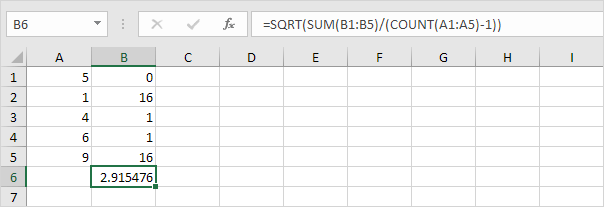
3. Felizmente, a função STDEV.S no Excel pode executar todas essas etapas para você.
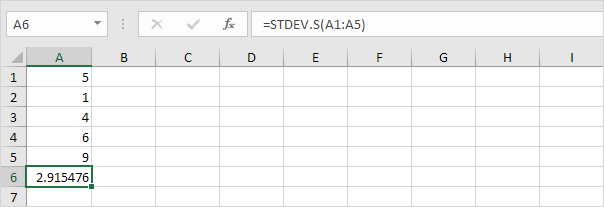
Nota: por que dividimos por n – 1 em vez de n quando estimamos o desvio padrão com base em uma amostra? A correção de Bessel afirma que dividir por n-1 em vez de n fornece uma estimativa melhor do desvio padrão.
Variância
A variância é o quadrado do desvio padrão. É muito simples. Às vezes, é mais fácil usar a variância ao resolver problemas estatísticos.
1. A função VAR.P abaixo calcula a variância com base em toda a população.
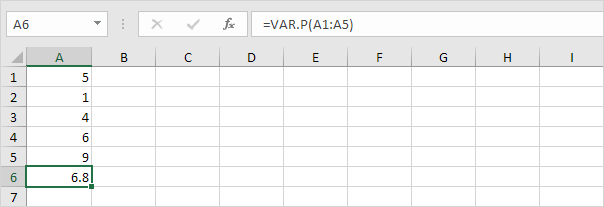
Observação: você já sabia esta resposta (consulte passo 5 em STDEV.P). Tire a raiz quadrada desse resultado para encontrar o desvio padrão com base em toda a população.
2. A função VAR.S abaixo estima a variação com base em uma amostra.
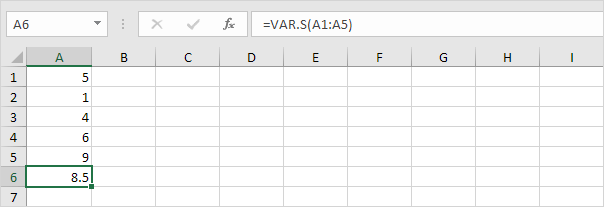
Observação: você já sabia esta resposta (consulte a etapa 1 sob STDEV.S). Tire a raiz quadrada desse resultado para encontrar o desvio padrão com base em uma amostra.
3. VAR e VAR.S produzem exatamente o mesmo resultado.
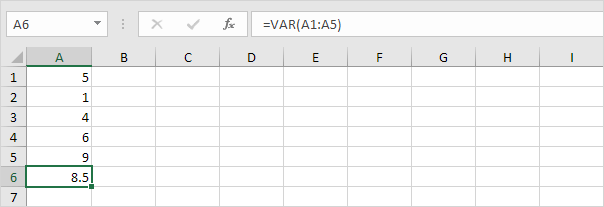
Observação: o Microsoft Excel recomenda o uso da nova função VAR.S.