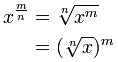Também chamados de “radicais” ou “expoentes racionais”
Expoentes de números inteiros
Primeiro, vejamos o número inteiro expoentes:

O expoente de um número diz quantas vezes usar o número em uma multiplicação.
Neste exemplo: 82 = 8 × 8 = 64
Outro exemplo: 53 = 5 × 5 × 5 = 125
Expoentes fracionais
Mas e se o expoente for uma fração?
|
Um expoente de 12 é na verdade a raiz quadrada Um expoente de 13 é a raiz cúbica Um expoente de 14 é a 4ª raiz E assim por diante! |
 |
Por quê?
Vejamos por que em um exemplo.
Primeiro, as Leis dos Expoentes nos dizem como lidar com os expoentes quando multiplicamos:
Exemplo: x2x2 = (xx) (xx) = xxxx = x4
O que mostra que x2x2 = x (2 + 2) = x4
Então, vamos tentar isso com expoentes fracionários:
Tente outra fração
Vamos tentar novamente, mas com um expoente de um quarto (1/4):
Exemplo:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Então 16¼ usado 4 vezes em uma multiplicação dá 16,
e então 16¼ é um 4ª raiz de 16
Regra geral
Funcionou por ½, funcionou com ¼, na verdade funciona geralmente:
x1 / n = A enésima raiz de x
Portanto, podemos chegar a isso:
| |
|
Exemplo: O que é 271/3?
Resposta: 271/3 = ![]() 27 = 3
27 = 3
E quanto às frações mais complicadas?
Que tal um expoente fracionário como 43/2?
Isso realmente significa fazer um cubo (3) e uma raiz quadrada (1/2), em qualquer ordem.
Deixe-me explicar.
Uma fração (como m / n) pode ser dividida em duas partes:
- uma parte de número inteiro (m) e
- uma fração (1 / n) parte
Então, porque m / n = m × (1 / n), podemos fazer isso:
A ordem não importa, então também funciona para m / n = (1 / n) × m:
E obtemos isso:
| |
|
Alguns exemplos:
Exemplo : O que é 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
ou
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
Qualquer uma das formas obtém o mesmo resultado.
Exemplo: O que é 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
ou
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Certamente foi mais fácil da segunda maneira!
Agora … Brinque com o gráfico!
Veja como a curva muda suavemente quando você brinca com as frações em Esta animação mostra que essa ideia de expoentes fracionários se encaixa perfeitamente:
Coisas para tentar:
- Comece com m = 1 e n = 1, depois aumente lentamente n para que você possa ver 1/2, 1/3 e 1/4
- Em seguida, tente m = 2 e deslize n para cima e para baixo para ver as frações como 2/3 etc
- Agora tente fazer o expoente -1
- Por último, tente aumentar m, reduzir n, reduzir m e aumentar n: a curva deve girar continuamente