A conjectura de Poincaré e 6 outras teorias matemáticas complexas foram apelidadas de Millennium Prize Problems pelo Clay Mathematics Institute (CMI). Cada problema foi descrito como uma “questão clássica importante que tem resistido a soluções ao longo dos anos”, com a primeira pessoa a conceber uma solução para cada um ganhando $ 1.000.000 por cortesia do CMI. No entanto, como você viu acima, resolver esses problemas não é fácil façanha. Um dos problemas permaneceu sem solução desde sua formulação em 1859 pelo matemático alemão Bernhard Riemann.
A hipótese de Riemann, em homenagem ao matemático alemão mencionado acima, é amplamente considerada o problema não resolvido mais importante em matemática. É de grande interesse na teoria dos números porque implica resultados sobre a distribuição dos números primos, que são usados em tudo, desde a biologia à criptografia e mecânica quântica. Para entender a hipótese de Riemann, primeiro precisamos explicar algumas chaves conceitos:
- Um número complexo tem a forma a + bi, onde i é definido por i² = -1. Nesta forma, a parte real de um número complexo é a, e o imaginário parte é bi.
- A função zeta de Riemann é uma função de uma variável complexa (uma função de números complexos) definida pela seguinte equação, onde s é qualquer número complexo diferente de 1, e cujos valores também são complexos:
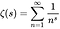
- Um “zero” de uma função é um x tal que f (x) = 0
- Os “zeros triviais” da função zeta de Riemann são todos os inteiros pares negativos (-2, -4, -6,…)
- Os “zeros não triviais ”Da função zeta de Riemann são todos os outros valores de s para os quais ζ (s) = 0 (ie. s não é um número inteiro negativo).
Agora que temos algumas definições, podemos prosseguir e declarar a hipótese de Riemann:
A parte real de cada zero não trivial da função zeta de Riemann é 1/2
Este (para mim pelo menos) é muito mais fácil de entender do que a Conjectura de Poincaré e não parece intuitivamente muito difícil. No entanto, também não parece significar muito. Na verdade, quem se importa quando essa função aleatória tem um valor de 0. Bem, não é de surpreender que muitos matemáticos tenham, e por um bom motivo.
Alguns números têm a propriedade especial de não poderem ser expressos como o produto de dois números menores (produto sendo multiplicação), ie. 2,3,5,7,11, etc. Conhecidos como números primos, eles são, em certo sentido, os números mais simples que você pode obter, formando os blocos de construção para todos os outros números. Frustrantemente, os números primos não parecem seguir nenhum padrão. 3137 é um número primo, e o próximo depois disso não é até 3163, mas então 3167 e 3169 seguem em rápida sucessão, todos os quais são primos. Em suma, se você encontrar um número primo, não há como saber onde o próximo estará sem verificar todos os números conforme você avança. No entanto, usando o teorema dos números primos (PNT), você pode descobrir quantos números primos existem abaixo de um certo limite.
O teorema dos números primos é apenas uma estimativa, com valores diferentes dando uma probabilidade diferente de ser correto, mas nunca com 100% de certeza. No entanto, entenda a suposição de que a hipótese de Reimann é verdadeira, você pode criar uma aproximação matemática combinando o Teorema dos Números Primos e os zeros não triviais da função zeta de Riemann para corrigir o erro dos componentes internos, fornecendo o “melhor possível” limite para o termo de erro no teorema dos números primos. Se fosse possível provar a hipótese de Reimann completamente, isso daria ao PNT a capacidade de fornecer estimativas incrivelmente próximas do valor real, abrindo muitas possibilidades em diferentes ramos da matemática. existem muitas hipóteses importantes de que estar com “Se a hipótese de Riemann for verdadeira, então …”, portanto, resolver esse problema validaria instantaneamente todas as conjecturas subsequentes também.