Exempel: slumpmässiga siffror
Antag att vi betraktar reella tal slumpmässigt valda mellan 0 och 1, som vi spelar in \ (X_1 \), det slumpmässiga talet trunkeras till en decimal. Exempelvis registreras siffran 0,07491234008 som 0,0 (som första decimal är noll). Observera att detta betyder att vi inte avrundar utan trunkerar. Om mekanismen som genererar dessa siffror inte har någon preferens för någon position i intervallet \ ((0,1) \), kommer fördelningen av siffrorna vi får att vara sådan att
\
Detta är en diskret slumpmässig variabel, med samma sannolikhet för vart och ett av de tio möjliga resultaten.
\
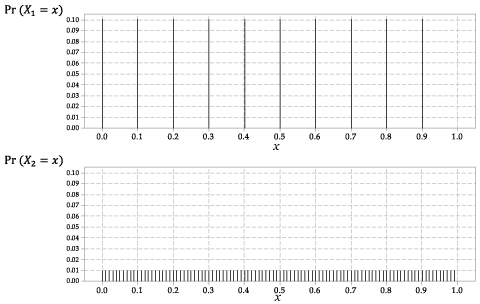
Fördelningarna av \ (X_1 \) och \ (X_2 \) visas i figur 2.
Detaljerad beskrivning
Figur 2: Sannolikhetsfunktionerna \ (p_ {X_1} (x) \) för \ (X_1 \) och \ (p_ {X_2} (x) \) för \ (X_2 \).
Excel har en funktion som ger verkliga tal mellan 0 och 1, så att det inte finns någon preferens för någon position i intervallet \ ( (0,1) \). Om du anger \ (\ sf \ text {= RAND ()} \) i en cell och trycker på Retur får du ett sådant nummer. Öka antalet decimaler som visas i cellen. Fortsätt tills du får många nollor i slutet av numret; du kan behöva öka cellens storlek. Ditt kalkylblad ska se ut som figur 3, men naturligtvis kommer det specifika numret att vara annorlunda … det är ju slumpmässigt!
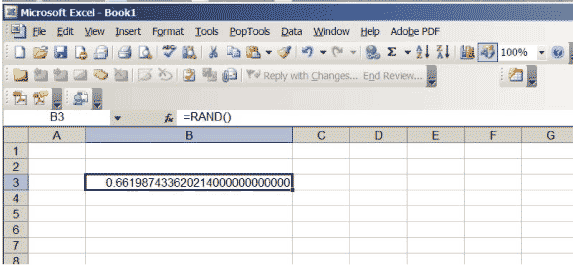
Figur 3: Ett Excel-kalkylblad med ett slumpmässigt tal mellan 0 och 1.
Om du trycker på tangenten ”F9” upprepade gånger vid den här tiden ser du en sekvens av slumpmässiga siffror, allt mellan 0 och 1. När man undersöker dessa verkar det som om Excel faktiskt producerar observationer på den slumpmässiga variabeln \ (X_ {15} \), de första 15 decimalerna i numret. Så chansen för att något specifikt av dessa nummer ska inträffa är \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ \ Pr (0.3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0.30) + \ Pr (X_2 = 0.31) + \ punkter + \ Pr (X_2 = 0.39) \\\\ & = 10 \ gånger 0.01 = 0.1, \\\\ \ Pr (0.3 \ leq X_3 < 0.4) & = 10 ^ 2 \ gånger 10 ^ {- 3} = 0,1, \\\\ \ Pr (0,3 \ leq X_4 < 0.4) & = 10 ^ 3 \ gånger 10 ^ {- 4} = 0,1, \\\\ & \ vdots \\\\ \ Pr (0,3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ gånger 10 ^ {- k} = 0.1, \\\\ & \ vdots \ end {align *}
När vi gör fördelningen finare och finare, med fler och fler möjliga diskreta värden, är sannolikheten att någon av dessa diskreta slumpmässiga variabler ligger i intervallet \ (
Till exempel \ (\ Pr (0.3 \ leq U \ leq 0.4) = 0.4 – 0.3 = 0.1 \).
Cdf för denna slumpmässiga variabel, \ (F_U (u) \), är därför mycket enkelt. Det är
\
Följande bild visar grafen för den kumulativa fördelningsfunktionen för \ (U \).
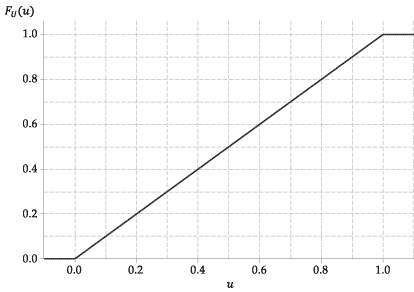
Figur 4: Den kumulativa fördelningsfunktionen för \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Du kanske har märkte en skillnad i hur intervallet mellan 0,3 och 0,4 behandlades i det kontinuerliga fallet, jämfört med de diskreta fallen. I alla diskreta fall exkluderades de övre gränserna \ (0,4, 0,40, 0,400, \ prickar \), medan den för den kontinuerliga slumpmässiga variabeln ingår. Närhelst vi har att göra med diskreta slumpmässiga variabler, oavsett om ojämlikheten är strikt eller inte, är det ofta viktigt och vård behövs. Till exempel
\ \