Eksempel: Tilfældige tal
Antag, at vi betragter reelle tal tilfældigt valgt mellem 0 og 1, som vi optager for \ (X_1 \), det tilfældige tal afkortet til en decimal. F.eks. Registreres tallet 0,07491234008 som 0,0 (som første decimal er nul). Bemærk, at dette betyder, at vi ikke afrunder, men trunkerer. Hvis mekanismen, der genererer disse tal, ikke foretrækker nogen position i intervallet \ ((0,1) \), vil fordelingen af de tal, vi får, være sådan, at
\
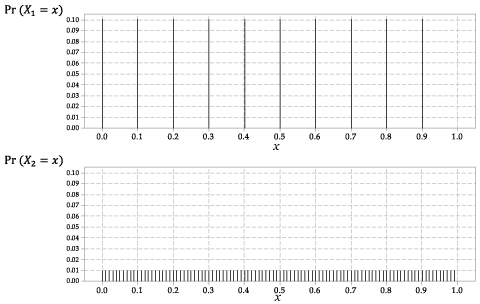
Dette er en diskret tilfældig variabel med samme sandsynlighed for hvert af de ti mulige resultater.
\
Fordelingen af \ (X_1 \) og \ (X_2 \) er vist i figur 2.
Detaljeret beskrivelse
Figur 2: Sandsynlighedsfunktionerne \ (p_ {X_1} (x) \) for \ (X_1 \) og \ (p_ {X_2} (x) \) for \ (X_2 \).
Excel har en funktion, der producerer reelle tal mellem 0 og 1, valgt således at der ikke foretrækkes nogen position i intervallet \ ( (0,1) \). Hvis du indtaster \ (\ sf \ text {= RAND ()} \) i en celle og trykker på retur, får du et sådant nummer. Forøg antallet af decimaler, der vises i cellen. Fortsæt, indtil du får mange nuller i slutningen af nummeret; Du skal muligvis øge størrelsen på cellen. Dit regneark skal se ud som figur 3, selvom det specifikke nummer naturligvis vil være anderledes … det er trods alt tilfældigt!
Figur 3: Et Excel-regneark med et tilfældigt tal fra mellem 0 og 1.
Hvis du trykker på tasten “F9” gentagne gange på dette tidspunkt, vil du se en række tilfældige tal, alt mellem 0 og 1. Fra at undersøge disse ser det ud til, at Excel faktisk producerer observationer på den tilfældige variabel \ (X_ {15} \), de første 15 decimaler i nummeret. Så chancen for, at et specifikt af disse tal opstår, er \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ \ Pr (0.3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0.30) + \ Pr (X_2 = 0.31) + \ prikker + \ Pr (X_2 = 0.39) \\\\ & = 10 \ gange 0.01 = 0.1, \\\\ \ Pr (0.3 \ leq X_3 < 0.4) & = 10 ^ 2 \ gange 10 ^ {- 3} = 0.1, \\\\ \ Pr (0,3 \ leq X_4 < 0,4) & = 10 ^ 3 \ gange 10 ^ {- 4} = 0,1, \\\\ & \ vdots \\\\ \ Pr (0,3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ gange 10 ^ {- k} = 0.1, \\\\ & \ vdots \ end {align *}
Da vi gør fordelingen finere og finere med flere og flere mulige diskrete værdier, er sandsynligheden for, at nogen af disse diskrete tilfældige variabler ligger i intervallet \ (
For eksempel \ (\ Pr (0,3 \ leq U \ leq 0,4) = 0,4 – 0,3 = 0,1 \).
Cdf’en for denne tilfældige variabel, \ (F_U (u) \), er derfor meget enkel. Det er
\
Følgende figur viser grafen for den kumulative fordelingsfunktion af \ (U \).
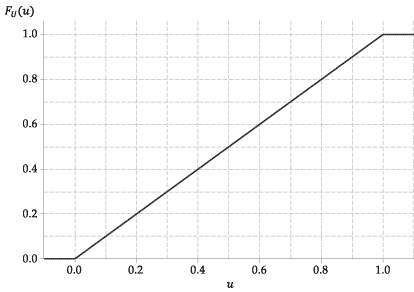
Figur 4: Den kumulative fordelingsfunktion af \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Du har muligvis bemærkede en forskel i, hvordan intervallet mellem 0,3 og 0,4 blev behandlet i det kontinuerlige tilfælde sammenlignet med de diskrete tilfælde. I alle de diskrete tilfælde blev de øvre grænser \ (0,4, 0,40, 0,400, \ prikker \) ekskluderet, mens den for den kontinuerlige tilfældige variabel er inkluderet. Hver gang vi har at gøre med diskrete tilfældige variabler, er det ofte vigtigt, om uligheden er streng eller ikke, og der er behov for omhu. For eksempel
\ \