Objectifs d’apprentissage
- Énoncez l’équation de l’onde de Broglie.
- Utilisation cette équation pour calculer la longueur d’onde d’un objet en mouvement.
Au-delà du modèle de Bohr
Le modèle de l’atome de Bohr a été utile pour démontrer comment les électrons étaient capables d’absorber et de libérer de l’énergie et comment les spectres d’émission atomique ont été créés. Cependant, le modèle n’expliquait pas vraiment pourquoi les électrons ne devraient exister que sur des orbites circulaires fixes plutôt que de pouvoir exister dans un nombre illimité d’orbites toutes avec des énergies différentes. Afin d’expliquer pourquoi les états d’énergie atomique sont quantifiés, les scientifiques devaient repenser la façon dont ils voyaient la nature de l’électron et son mouvement.
L’investigation de Planck sur les spectres d’émission des objets chauds et les études ultérieures sur l’effet photoélectrique avaient prouvé que la lumière était capable de se comporter à la fois comme une onde et comme une particule. Il semblait raisonnable de se demander si les électrons pouvaient également avoir une nature double onde-particule. En 1924, le scientifique français Louis de Broglie (1892–1987) a dérivé une équation décrivant la nature ondulatoire de toute particule. En particulier, la longueur d’onde (λ) de tout objet en mouvement est donnée par:
\ displaystyle \ lambda = \ frac {h} {mv}
Dans cette équation, h est la constante de Planck , m est la masse de la particule en kg, et v est la vitesse de la particule en m / s. Le problème ci-dessous montre comment calculer la longueur d’onde de l’électron.
Si nous devions calculer la longueur d’onde d’une balle de baseball de 0,145 kg lancée à une vitesse de 40 m / s, nous arriverions à un très court longueur d’onde de l’ordre de 10−34 m. Cette longueur d’onde est impossible à détecter même avec un équipement scientifique de pointe. En effet, alors que tous les objets bougent avec un mouvement ondulatoire, nous ne le remarquons jamais car les longueurs d’onde sont beaucoup trop courtes. D’un autre côté, les particules avec des longueurs d’onde mesurables sont toutes très petites. Cependant, la nature ondulatoire de l’électron s’est avérée être un développement clé dans une nouvelle compréhension de la nature de l’électron. Un électron qui est confiné à un espace particulier autour du noyau d’un atome ne peut se déplacer autour de cet atome que de telle sorte que son onde électronique «s’adapte» correctement à la taille de l’atome. Cela signifie que les fréquences des ondes électroniques sont quantifiées. Sur la base de l’équation E = hv, les fréquences quantifiées signifient que les électrons ne peuvent exister dans un atome qu’à des énergies spécifiques, comme Bohr l’avait précédemment théorisé.
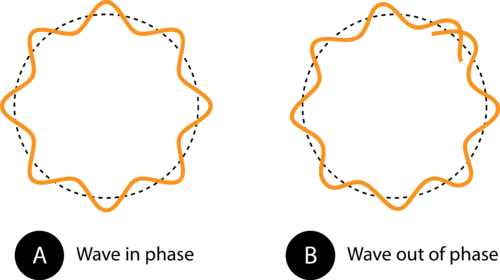
Figure 1. La circonférence de l’orbite en (A) permet à l’onde d’électrons de s’intégrer parfaitement dans l’orbite. C’est une orbite autorisée. En (B), l’onde d’électrons ne s’intègre correctement dans l’orbite, donc cette orbite n’est pas autorisée.
Résumé
- Les équations d’onde deBroglie permettent de calculer la longueur d’onde de tout mouvement objet.
- Lorsque la vitesse de l’électron diminue, sa longueur d’onde augmente.
Pratique
Utilisez le lien ci-dessous pour pratiquer les calculs en utilisant l’équation de l’onde deBroglie:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Examen
- Quoi le modèle de Bohr n’a-t-il pas expliqué?
- Énoncez l’équation de l’onde deBroglie.
- Que se passe-t-il lorsque la vitesse de l’électron diminue?