Példa: Véletlenszerű számok
Tegyük fel, hogy véletlenszerűen 0 és 1 között választott valós számokat veszünk figyelembe, amelyekhez rögzítjük \ (X_1 \), a véletlenszerű szám egy tizedesjegyig csonkítva. Például a 0.07491234008 számot 0.0-ként rögzítjük (mivel az első tizedesjegy nulla). Vegye figyelembe, hogy ez azt jelenti, hogy nem kerekítünk, hanem csonkítunk. Ha az ezeket a számokat létrehozó mechanizmus nem preferál semmilyen helyet az \ ((0,1) \) intervallumban, akkor a számok eloszlása olyan lesz, hogy
\
Ez egy diszkrét véletlenszerű változó, azonos valószínűséggel a tíz lehetséges eredmény mindegyikéhez.
\
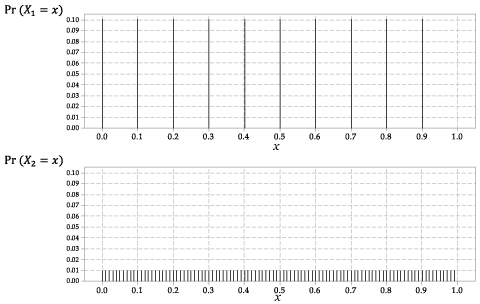
Az \ (X_1 \) és \ (X_2 \) eloszlását a 2. ábra mutatja.
Részletes leírás
2. ábra: A \ (X_1 \) és \ (p_) valószínűségi függvények \ (p_ {X_1} (x) \) {X_2} (x) \) a (z) (X_2 \) kifejezéshez.
Az Excel olyan funkcióval rendelkezik, amely 0 és 1 közötti valós számokat állít elő, úgy választva, hogy az intervallum egyetlen pozícióját sem részesítse előnyben \ ( (0,1) \). Ha egy cellába beírja a \ (\ sf \ text {= RAND ()} \) elemet, és a return gombra kattint, akkor ilyen számot kap. Növelje a cellában látható tizedesjegyek számát. Folytasd addig, amíg sok nullát nem kapsz a szám végén; lehet, hogy növelnie kell a cella méretét. A táblázatnak úgy kell kinéznie, mint a 3. ábra, bár természetesen a konkrét szám más lesz … végül is véletlenszerű!
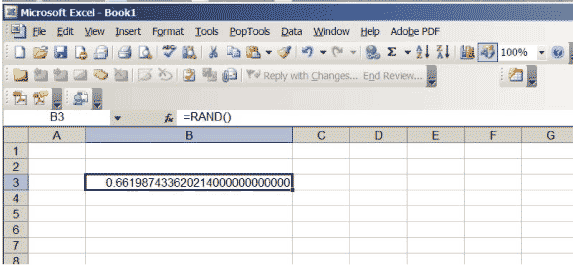
3. ábra: Excel-táblázat 0 és 1 közötti véletlenszerű számmal.
Ha ezen a ponton többször megnyomja az „F9” billentyűt, akkor véletlenszerű számok sorozata jelenik meg, mind 0 és 1. Ezek vizsgálatából kiderül, hogy az Excel valóban megfigyeléseket készít a véletlen változón ((X_ {15} \), a szám első 15 tizedesjegyén). Tehát a számok bármelyikének előfordulási esélye \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ \ Pr (0.3 \ leq X_2 < 0,4) & = \ Pr (X_2 = 0,30) + \ Pr (X_2 = 0,31) + \ pontok + \ Pr (X_2 = 0,39) \\\\ & = 10 \ szor 0,01 = 0,1, \\\\ \ Pr (0,3 \ leq X_3 < 0,4) & = 10 ^ 2 \ szor 10 ^ {- 3} = 0,1, \\\\ \ Pr (0,3 \ leq X_4 < 0,4) & = 10 ^ 3 \ szor 10 ^ {- 4} = 0,1, \\\\ & \ vdots \\\\ Pr (0,3 \ leq X_k < 0,4) & = 10 ^ {k-1} 10-szer 10 ^ {- k} = 0,1, \\\\ & \ vdots \ end {align *}
Amint az elosztást egyre finomabbá tesszük, minél több diszkrét értékkel, annak valószínűsége, hogy ezek a diszkrét véletlen változók bármelyike a \ (
Például \ (\ Pr (0,3 \ leq U \ leq 0,4) = 0,4 – 0,3 = 0,1 \).
Ennek a véletlen változónak a cdf-je, \ (F_U (u) \), ezért nagyon egyszerű. Ez
\
A következő ábra az \ (U \) kumulatív eloszlásfüggvényének grafikonját mutatja.
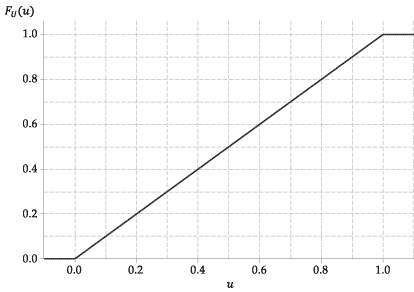
4. ábra: A \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \) kumulatív elosztási függvénye.
Lehet, hogy különbséget észlelt abban, hogy a 0,3 és 0,4 közötti intervallumot hogyan kezelték a folyamatos esetben, a diszkrét esetekhez képest. Az összes diszkrét esetben kizártuk a felső határokat (0,4, 0,40, 0,400, \ pontok), míg a folytonos véletlenszerű változóhoz. Amikor diszkrét véletlenszerű változókkal van dolgunk, gyakran számít az, hogy szigorú-e az egyenlőtlenség, vagy nem, és körültekintésre van szükség. Például:
\ \