Voorbeeld: willekeurige getallen
Stel dat we reële getallen beschouwen als willekeurig gekozen tussen 0 en 1, waarvoor we opnemen \ (X_1 \), het willekeurige getal afgekapt tot één decimaal. Het getal 0,07491234008 wordt bijvoorbeeld geregistreerd als 0,0 (aangezien de eerste decimaal nul is). Merk op dat dit betekent dat we niet afronden, maar afkappen. Als het mechanisme dat deze getallen genereert, geen voorkeur heeft voor een positie in het interval \ ((0,1) \), dan zal de verdeling van de getallen die we verkrijgen zodanig zijn dat
\
Dit is een discrete willekeurige variabele, met dezelfde waarschijnlijkheid voor elk van de tien mogelijke uitkomsten.
\
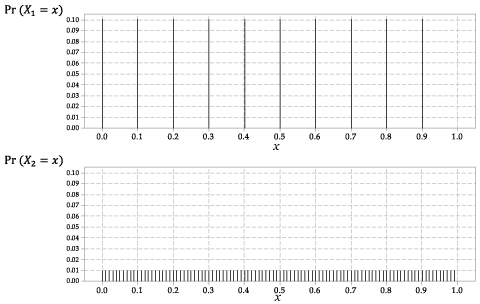
De verdelingen van \ (X_1 \) en \ (X_2 \) worden weergegeven in figuur 2.
Gedetailleerde beschrijving
Figuur 2: De waarschijnlijkheidsfuncties \ (p_ {X_1} (x) \) voor \ (X_1 \) en \ (p_ {X_2} (x) \) voor \ (X_2 \).
Excel heeft een functie die reële getallen tussen 0 en 1 produceert, zo gekozen dat er geen voorkeur is voor een positie in het interval \ ( (0,1) \). Als je \ (\ sf \ text {= RAND ()} \) in een cel invoert en op Return drukt, krijg je zo’n nummer. Verhoog het aantal decimalen dat in de cel wordt weergegeven. Blijf doorgaan totdat u veel nullen aan het einde van het getal krijgt; Mogelijk moet u de cel vergroten. Uw spreadsheet zou eruit moeten zien als figuur 3, hoewel het specifieke nummer natuurlijk anders zal zijn … het is tenslotte willekeurig!
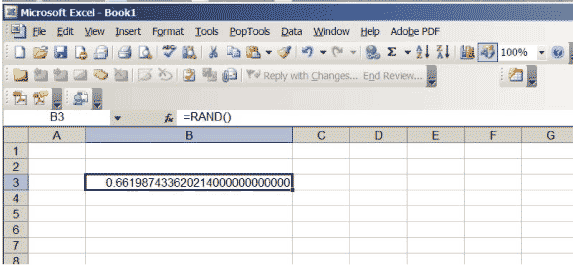
Figuur 3: een Excel-spreadsheet met een willekeurig getal tussen 0 en 1.
Als u op dit punt herhaaldelijk op de toets “F9” drukt, ziet u een reeks willekeurige getallen, allemaal tussen 0 en 1. Uit deze onderzoeken blijkt dat Excel feitelijk waarnemingen produceert op de willekeurige variabele \ (X_ {15} \), de eerste 15 decimalen van het getal. Dus de kans dat een van deze getallen voorkomt is \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ \ Pr (0.3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0.30) + \ Pr (X_2 = 0.31) + \ dots + \ Pr (X_2 = 0.39) \\\\ & = 10 \ times 0.01 = 0.1, \\\\ \ Pr (0.3 \ leq X_3 < 0.4) & = 10 ^ 2 \ times 10 ^ {- 3} = 0.1, \\\\ \ Pr (0.3 \ leq X_4 < 0.4) & = 10 ^ 3 \ maal 10 ^ {- 4} = 0.1, \\\\ & \ vdots \\\\ \ Pr (0.3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ maal 10 ^ {- k} = 0.1, \\\\ & \ vdots \ end {align *}
Naarmate we de verdeling fijner en fijner maken, met steeds meer mogelijke discrete waarden, is de kans dat een van deze discrete willekeurige variabelen in het interval ligt \ (
Bijvoorbeeld, \ (\ Pr (0.3 \ leq U \ leq 0.4) = 0.4 – 0.3 = 0.1 \).
De cdf van deze willekeurige variabele, \ (F_U (u) \), is daarom heel eenvoudig. Het is
\
De volgende afbeelding toont de grafiek van de cumulatieve verdelingsfunctie van \ (U \).
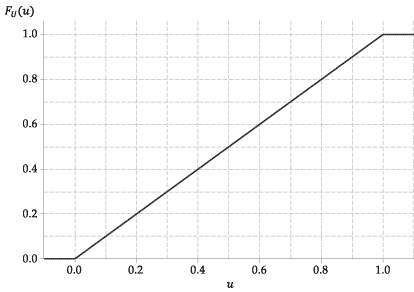
Figuur 4: De cumulatieve verdelingsfunctie van \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Misschien heb je merkte een verschil op in hoe het interval tussen 0,3 en 0,4 werd behandeld in het continue geval, vergeleken met de discrete gevallen. In alle discrete gevallen zijn de bovengrenzen \ (0.4, 0.40, 0.400, \ dots \) uitgesloten, terwijl deze voor de continue willekeurige variabele is opgenomen. Wanneer we te maken hebben met discrete willekeurige variabelen, is het vaak van belang of de ongelijkheid strikt is of niet, en is voorzichtigheid geboden. Bijvoorbeeld
\ \