Objetivos de aprendizagem
- Enuncie a equação de onda de de Broglie.
- Use esta equação para calcular o comprimento de onda de um objeto em movimento.
Além do modelo de Bohr
O modelo do átomo de Bohr foi valioso para demonstrar como os elétrons foram capazes de absorver e liberar energia e como os espectros de emissão atômica foram criados. No entanto, o modelo não explicava realmente por que os elétrons deveriam existir apenas em órbitas circulares fixas, em vez de serem capazes de existir em um número ilimitado de órbitas, todas com energias diferentes. Para explicar por que os estados de energia atômica são quantizados, os cientistas precisaram repensar a maneira como eles viam a natureza do elétron e seu movimento.
A investigação de Planck dos espectros de emissão de objetos quentes e os estudos subsequentes sobre o efeito fotoelétrico provaram que a luz era capaz de se comportar tanto como onda quanto como partícula. Parecia razoável imaginar se os elétrons também poderiam ter uma natureza de partícula de onda dupla. Em 1924, o cientista francês Louis de Broglie (1892–1987) derivou uma equação que descreve a natureza ondulatória de qualquer partícula. Particularmente, o comprimento de onda (λ) de qualquer objeto em movimento é dado por:
\ displaystyle \ lambda = \ frac {h} {mv}
Nesta equação, h é a constante de Planck , m é a massa da partícula em kg ev é a velocidade da partícula em m / s. O problema abaixo mostra como calcular o comprimento de onda do elétron.
Se fossemos calcular o comprimento de onda de uma bola de beisebol de 0,145 kg lançada a uma velocidade de 40 m / s, chegaríamos a um extremamente curto comprimento de onda da ordem de 10−34 m. Este comprimento de onda é impossível de detectar, mesmo com equipamentos científicos avançados. Na verdade, embora todos os objetos se movam com movimento ondulatório, nunca o notamos porque os comprimentos de onda são curtos demais. Por outro lado, as partículas com comprimentos de onda mensuráveis são todas muito pequenas. No entanto, a natureza ondulatória do elétron provou ser um desenvolvimento fundamental para uma nova compreensão da natureza do elétron. Um elétron que está confinado a um determinado espaço ao redor do núcleo de um átomo só pode se mover ao redor desse átomo de forma que sua onda de elétrons “se ajuste” ao tamanho do átomo corretamente. Isso significa que as frequências das ondas de elétrons são quantizadas. Com base na equação E = hv, as frequências quantizadas significam que os elétrons só podem existir em um átomo com energias específicas, como Bohr havia teorizado anteriormente.
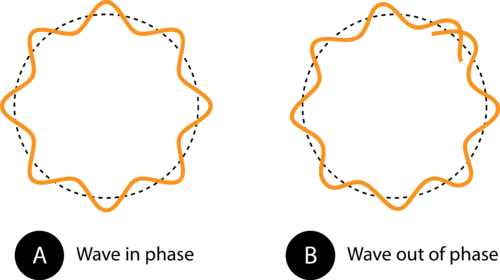
Figura 1. A circunferência da órbita em (A) permite que a onda de elétrons se encaixe perfeitamente na órbita. Esta é uma órbita permitida. Em (B), a onda de elétrons não se encaixam adequadamente na órbita, portanto, esta órbita não é permitida.
Resumo
- As equações de onda deBroglie permitem o cálculo do comprimento de onda de qualquer movimento objeto.
- Conforme a velocidade do elétron diminui, seu comprimento de onda aumenta.
Pratique
Use o link abaixo para praticar cálculos usando a equação da onda deBroglie:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Revisão
- O que o modelo de Bohr não explicou?
- Enuncie a equação da onda deBroglie.
- O que acontece quando a velocidade do elétron diminui?