Exemplu: numere aleatorii
Să presupunem că considerăm numere reale alese aleatoriu între 0 și 1, pentru care înregistrăm \ (X_1 \), numărul aleatoriu trunchiat la o zecimală. De exemplu, numărul 0,07491234008 este înregistrat ca 0,0 (deoarece prima zecimală este zero). Rețineți că acest lucru înseamnă că nu suntem rotunjitori, ci tăiați. Dacă mecanismul care generează aceste numere nu are nicio preferință pentru nicio poziție în intervalul \ ((0,1) \), atunci distribuția numerelor pe care le obținem va fi astfel încât
\
Acesta este un aleatoriu discret variabilă, cu aceeași probabilitate pentru fiecare dintre cele zece rezultate posibile.
\
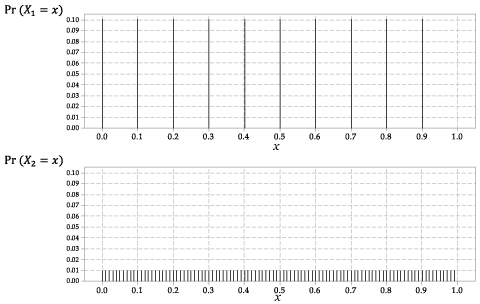
Distribuțiile lui \ (X_1 \) și \ (X_2 \) sunt prezentate în figura 2.
Descriere detaliată
Figura 2: Funcțiile de probabilitate \ (p_ {X_1} (x) \) pentru \ (X_1 \) și \ (p_ {X_2} (x) \) pentru \ (X_2 \).
Excel are o funcție care produce numere reale între 0 și 1, aleasă astfel încât să nu existe nicio preferință pentru nicio poziție din intervalul \ ( (0,1) \). Dacă introduceți \ (\ sf \ text {= RAND ()} \) într-o celulă și apăsați return, veți obține un astfel de număr. Măriți numărul de zecimale afișate în celulă. Continuați până când veți obține o mulțime de zero la sfârșitul numărului; s-ar putea să fie nevoie să măriți dimensiunea celulei. Foaia dvs. de calcul ar trebui să arate ca figura 3, deși, desigur, numărul specific va fi diferit … este la întâmplare, la urma urmei!
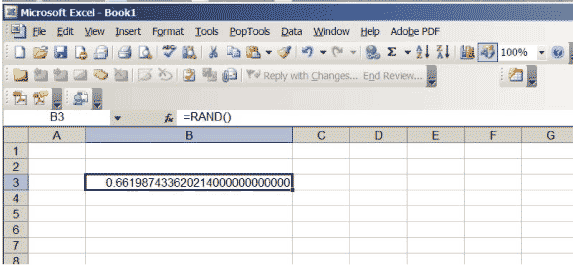
Figura 3: O foaie de calcul Excel cu un număr aleatoriu între 0 și 1.
Dacă apăsați tasta „F9” în mod repetat în acest moment, veți vedea o secvență de numere aleatoare, toate între 0 și 1. Din examinarea acestora, se pare că Excel produce de fapt observații asupra variabilei aleatorii \ (X_ {15} \), primele 15 zecimale ale numărului. Deci, șansa apariției unuia dintre aceste numere este \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0.4) & = \ Pr (X_1 = 0.3) = 0.1, \\\\ \ Pr (0.3 \ leq X_2 < 0.4) & = \ Pr (X_2 = 0.30) + \ Pr (X_2 = 0.31) + \ dots + \ Pr (X_2 = 0.39) \\\\ & = 10 \ times 0.01 = 0.1, \\\\ \ Pr (0.3 \ leq X_3 < 0.4) & = 10 ^ 2 \ times 10 ^ {- 3} = 0.1, \\\\ \ Pr (0.3 \ leq X_4 < 0.4) & = 10 ^ 3 \ times 10 ^ {- 4} = 0.1, \\\\ & \ vdots \\\\ \ Pr (0.3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ times 10 ^ {- k} = 0.1, \\\\ & \ vdots \ end {align *}
Pe măsură ce distribuția este mai fină, cu valori discrete din ce în ce mai posibile, probabilitatea ca oricare dintre aceste variabile aleatorii discrete să se afle în interval \ (
De exemplu, \ (\ Pr (0.3 \ leq U \ leq 0.4) = 0.4 – 0.3 = 0.1 \).
Cdf-ul acestei variabile aleatoare, \ (F_U (u) \), este deci foarte simplu. Este
\
Figura următoare prezintă graficul funcției de distribuție cumulativă a \ (U \).
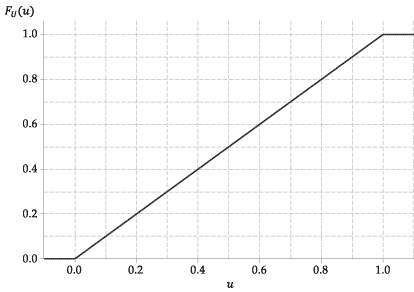
Figura 4: Funcția de distribuție cumulativă a \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Este posibil să aveți am observat o diferență în modul în care intervalul dintre 0,3 și 0,4 a fost tratat în cazul continuu, comparativ cu cazurile discrete. În toate cazurile discrete, limitele superioare \ (0,4, 0,40, 0,400, \ puncte \) au fost excluse, în timp ce pentru variabila continuă aleatorie este inclusă. Ori de câte ori avem de-a face cu variabile aleatorii discrete, indiferent dacă inegalitatea este strictă sau nu contează adesea, este nevoie de îngrijire. De exemplu,
\ \