Exemple: nombres aléatoires
Supposons que nous considérions des nombres réels choisis au hasard entre 0 et 1, pour lesquels nous enregistrons \ (X_1 \), le nombre aléatoire tronqué à une décimale. Par exemple, le nombre 0,07491234008 est enregistré comme 0,0 (la première décimale étant zéro). Notez que cela signifie que nous ne sommes pas arrondis, mais tronqués. Si le mécanisme générant ces nombres n’a de préférence pour aucune position dans l’intervalle \ ((0,1) \), alors la distribution des nombres que nous obtenons sera telle que
\
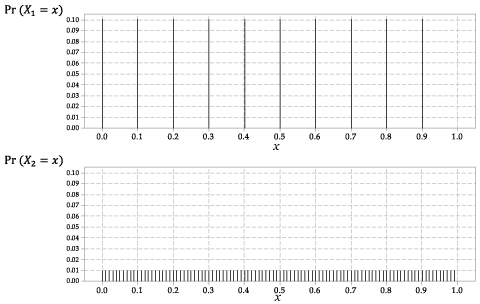
Ceci est un aléatoire discret variable, avec la même probabilité pour chacun des dix résultats possibles.
\
Les distributions de \ (X_1 \) et \ (X_2 \) sont présentées dans la figure 2.
Description détaillée
Figure 2: Les fonctions de probabilité \ (p_ {X_1} (x) \) pour \ (X_1 \) et \ (p_ {X_2} (x) \) pour \ (X_2 \).
Excel a une fonction qui produit des nombres réels entre 0 et 1, choisis de sorte qu’il n’y ait aucune préférence pour aucune position dans l’intervalle \ ( (0,1) \). Si vous entrez \ (\ sf \ text {= RAND ()} \) dans une cellule et appuyez sur retour, vous obtiendrez un tel nombre. Augmentez le nombre de décimales affichées dans la cellule. Continuez jusqu’à ce que vous obteniez beaucoup de zéros à la fin du nombre; vous devrez peut-être augmenter la taille de la cellule. Votre feuille de calcul devrait ressembler à la figure 3, même si bien sûr le nombre spécifique sera différent… il est aléatoire, après tout!
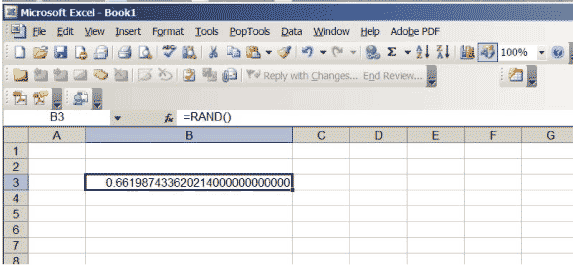
Figure 3: Une feuille de calcul Excel avec un nombre aléatoire compris entre 0 et 1.
Si vous appuyez plusieurs fois sur la touche «F9» à ce stade, vous verrez une séquence de nombres aléatoires, tous compris entre 0 et 1. En les examinant, il apparaît qu’Excel produit en fait des observations sur la variable aléatoire \ (X_ {15} \), les 15 premières décimales du nombre. Ainsi, la probabilité qu’un de ces nombres se produise est \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0,4) & = \ Pr (X_1 = 0,3) = 0,1, \\\\ \ Pr (0,3 \ leq X_2 < 0,4) & = \ Pr (X_2 = 0,30) + \ Pr (X_2 = 0,31) + \ dots + \ Pr (X_2 = 0,39) \\\\ & = 10 \ fois 0,01 = 0,1, \\\\ \ Pr (0,3 \ leq X_3 < 0,4) & = 10 ^ 2 \ times 10 ^ {- 3} = 0,1, \\\\ \ Pr (0,3 \ leq X_4 < 0,4) & = 10 ^ 3 \ fois 10 ^ {- 4} = 0,1, \\\\ & \ vdots \\\\ \ Pr (0,3 \ leq X_k < 0.4) & = 10 ^ {k-1} \ times 10 ^ {- k} = 0,1, \\\\ & \ vdots \ end {align *}
À mesure que nous rendons la distribution de plus en plus fine, avec de plus en plus de valeurs discrètes possibles, la probabilité qu’une de ces variables aléatoires discrètes se trouve dans l’intervalle \ (
Par exemple, \ (\ Pr (0.3 \ leq U \ leq 0.4) = 0.4 – 0.3 = 0.1 \).
Le cdf de cette variable aléatoire, \ (F_U (u) \), est donc très simple. C’est
\
La figure suivante montre le graphique de la fonction de distribution cumulative de \ (U \).
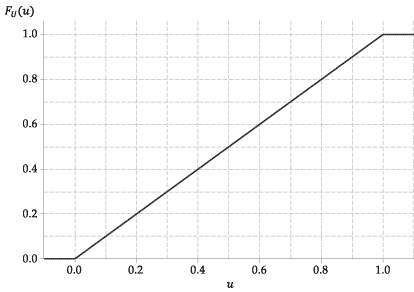
Figure 4: La fonction de distribution cumulative de \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Vous pourriez avoir remarqué une différence dans la façon dont l’intervalle entre 0,3 et 0,4 a été traité dans le cas continu, par rapport aux cas discrets. Dans tous les cas discrets, les limites supérieures \ (0,4, 0,40, 0,400, \ points \) ont été exclues, tandis que pour la variable aléatoire continue, elle est incluse. Chaque fois que nous avons affaire à des variables aléatoires discrètes, le fait que l’inégalité soit stricte ou peu importe souvent, et il faut être prudent. Par exemple,
\ \