Exemplo: Números aleatórios
Suponha que consideremos números reais escolhidos aleatoriamente entre 0 e 1, para os quais registramos \ (X_1 \), o número aleatório truncado em uma casa decimal. Por exemplo, o número 0,07491234008 é registrado como 0,0 (já que a primeira casa decimal é zero). Observe que isso significa que não estamos arredondando, mas truncando. Se o mecanismo que gera esses números não tem preferência por nenhuma posição no intervalo \ ((0,1) \), então a distribuição dos números que obtemos será tal que
\
Este é um aleatório discreto variável, com a mesma probabilidade para cada um dos dez resultados possíveis.
\
As distribuições de \ (X_1 \) e \ (X_2 \) são mostradas na figura 2.
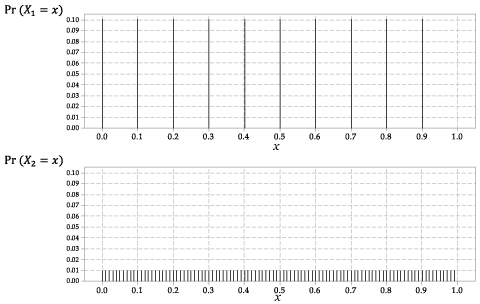
Descrição detalhada
Figura 2: As funções de probabilidade \ (p_ {X_1} (x) \) para \ (X_1 \) e \ (p_ {X_2} (x) \) para \ (X_2 \).
O Excel possui uma função que produz números reais entre 0 e 1, escolhidos de forma que não haja preferência por nenhuma posição no intervalo \ ( (0,1) \). Se você inserir \ (\ sf \ text {= RAND ()} \) em uma célula e clicar em Enter, você obterá esse número. Aumente o número de casas decimais mostradas na célula. Continue indo até obter muitos zeros no final do número; pode ser necessário aumentar o tamanho da célula. Sua planilha deve se parecer com a figura 3, embora é claro que o número específico será diferente … afinal, é aleatório!
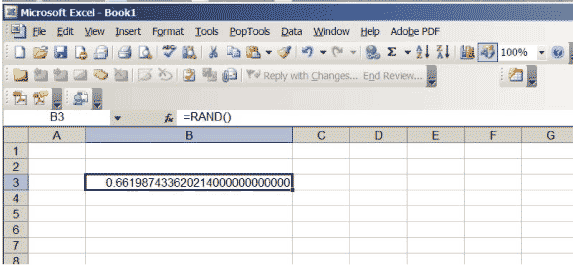
Figura 3: uma planilha Excel com um número aleatório entre 0 e 1.
Se você pressionar a tecla “F9” repetidamente neste ponto, verá uma sequência de números aleatórios, todos entre 0 e 1. Ao examiná-los, parece que o Excel realmente produz observações sobre a variável aleatória \ (X_ {15} \), as primeiras 15 casas decimais do número. Portanto, a chance de qualquer um desses números específicos ocorrer é \ (10 ^ {- 15} \).
\ begin {align *} \ Pr (0.3 \ leq X_1 < 0,4) & = \ Pr (X_1 = 0,3) = 0,1, \\\\ \ Pr (0,3 \ leq X_2 < 0,4) & = \ Pr (X_2 = 0,30) + \ Pr (X_2 = 0,31) + \ dots + \ Pr (X_2 = 0,39) \\\\ & = 10 \ vezes 0,01 = 0,1, \\\\ \ Pr (0,3 \ leq X_3 < 0,4) & = 10 ^ 2 \ vezes 10 ^ {- 3} = 0,1, \\\\ \ Pr (0,3 \ leq X_4 < 0,4) & = 10 ^ 3 \ vezes 10 ^ {- 4} = 0,1, \\\\ & \ vdots \\\\ \ Pr (0,3 \ leq X_k < 0,4) & = 10 ^ {k-1} \ vezes 10 ^ {- k} = 0,1, \\\\ & \ vdots \ end {align *}
À medida que tornamos a distribuição cada vez mais precisa, com cada vez mais valores discretos possíveis, a probabilidade de que qualquer uma dessas variáveis aleatórias discretas esteja no intervalo \ (
Por exemplo, \ (\ Pr (0.3 \ leq U \ leq 0.4) = 0.4 – 0.3 = 0.1 \).
O cdf desta variável aleatória, \ (F_U (u) \), é, portanto, muito simples. É
\
A figura a seguir mostra o gráfico da função de distribuição cumulativa de \ (U \).
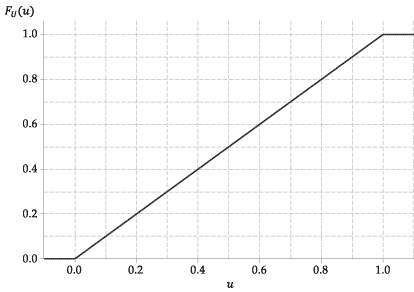
Figura 4: A função de distribuição cumulativa de \ (U \ stackrel {\ mathrm {d}} {=} \ mathrm {U} (0,1) \).
Você pode ter notaram diferença no tratamento do intervalo entre 0,3 e 0,4 no caso contínuo, em comparação com os casos discretos. Em todos os casos discretos, os limites superiores \ (0,4, 0,40, 0,400, \ pontos \) foram excluídos, enquanto para a variável aleatória contínua ele foi incluído. Sempre que estamos lidando com variáveis aleatórias discretas, se a desigualdade é estrita ou não, é sempre importante e é necessário cuidado. Por exemplo,
\ \